Circular Motion Explained
Circular motion is a very important concept in physics. Here on this page, I would like to go through the concept of circular motion. You encounter circular motion in your day-to-day life. Many rides in amusement parks undergo circular motion. Curves on highways are part of a circle and cars making a tun undergoes circular motion. Merry-go-Rounds in playgrounds offer further examples of uniform circular motion. Now let us learn more about circular motion.
Now when a particle moves along a circular path it must-have components of acceleration perpendicular to the path when its speed is constant. Such a type of circular motion is called Uniform circular motion. For this article consider the particle moves in a circular path with constant speed. Here in this article, we will discuss how to drive the relation between the normal component of acceleration, the particle’s speed, and the radius of the path.
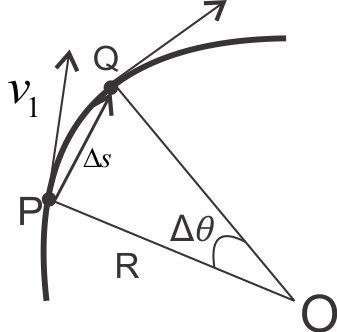
To understand this consider the figure given below
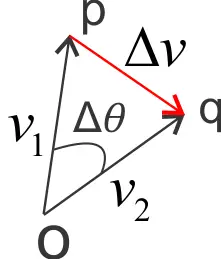
This figure represents a particle that is moving in a circular path of radius $R$ and has its center at $O$. Here vectors $v_{1}$ and $v_{2}$ represent the velocities at points P and Q respectively. The figure given below shows the vector change in velocity that is $\Delta v$ as the particle moves from $P$ to $Q$ in time $\Delta t$.
The triangle $OPQ$ in the first figure and triangle $opq$ in the second figure are similar since both are isosceles triangles and the angles labeled $\Delta \theta$ in both the triangles are the same. Hence we have
$ \frac{\Delta v}{v_{1}}=\frac{\Delta s}{R} $
or
$\Delta v=\frac{v_{1}}{R}\Delta s$
Let $|a_{\perp }|$ be the magnitude of average normal acceleration during time $\Delta t$ and is equal to $\frac{\Delta v}{\Delta t}$. So from above equation we get
$|a_{\perp}|=\frac{\Delta v}{\Delta t}=\frac{v_{1}}{R} \frac{\Delta s}{\Delta t}$
So the instantaneous acceleration $a_{\perp}$ at point $P$ is the limiting value of this expression as we take point $Q$ to point $P$ and $\Delta t \rightarrow 0$
So,
${a_ \bot } = \mathop {\lim }\limits_{\Delta t \to 0} \left( {\frac{{{v_1}}}{R}\frac{{\Delta s}}{{\Delta t}}} \right) = \frac{{{v_1}}}{R}\mathop {\lim }\limits_{\Delta t \to 0} \left( {\frac{{\Delta s}}{{\Delta t}}} \right)$
But the limiting value of ${\frac{{\Delta s}}{{\Delta t}}}$ is the speed ${{v_1}}$ of the particle at point $P$ . Since $P$ can be any point in the path , we can conveniently drop the subscript from ${{v_1}}$ and let $v$ represents the speed of the particle at any point in the circular path. So
${a_ \bot }=\frac{{{v^2}}}{R}$
So , from the above equation we can say that
The magnitude of the instantaneous normal acceleration is equal to the square of the speed divided by the radius. Its direction is perpendicular to $v$ and acts along inward direction along the radius of the circular path towards the center of the circle.
Because of this, it is called central or centripetal acceleration. The term centripetal means seeking the center.
So far we have discussed circular motion physics with particles moving with constant speed. If the speed varies then the above equation for normal acceleration or centripetal acceleration still holds but in the case of varying speed you also have a tangential component of acceleration ${a_\parallel }$, equal to the rate of change of speed. So,
${a_\parallel } = \mathop {\lim }\limits_{\Delta t \to 0} \left( {\frac{{\Delta {v_\parallel }}}{{\Delta t}}} \right)$
So if the speed is constant then there is no tangential acceleration. In this case, acceleration is purely normal. This normal acceleration is the result of the continuous change in direction of the velocity.
Forces causing Centripetal acceleration
We know that it is Newton’s second law that governs circular motion as well as other motions of the particle. Centripetal acceleration acts towards the center of the circular path for a particle moving in a uniform circular motion. This centripetal acceleration is caused by the force that is also directed towards the center. Since the magnitude of centripetal acceleration is equal to (\frac{{{v^2}}}{R}) , and it is directed towards the center, the magnitude of the force on a particle of mass $m$ would be,
$F = m{a_ \bot } = m\frac{{{v^2}}}{R}$
One of the familiar examples of such kind of force is the one when you tie a stone to a string and you whirl it. The string must constantly pull towards the center and if it breaks then there is no inwards force acting on the stone. At this point, the stoneflies off along a tangent to the circle.
One important thing to note here is that the term “centripetal force,” gives us a mistaken impression that it is a new force of nature. In reality, it is not. The adjective “centripetal” in “centripetal force” simply means that the force in question acts toward a center for example string tension on a tetherball or gravity on a satellite. A centripetal force must be supplied by some actual, physical force.
Related Articles
Acceleration formula Explained with Examples
 Skip to content
Skip to content