Atwood machine

An Atwood machine is a common physics problem involving a system of two masses connected by a string that passes over a pulley. The problems typically revolve around finding the acceleration of the masses and the tension in the string.

Introduction

The Atwood machine was invented in 1784 by Rev. George Atwood as a laboratory experiment to verify the mechanical laws of motion with constant acceleration. Atwood’s machine is a common classroom demonstration used to illustrate principles of classical mechanics.

Description of Atwood Machine

The ideal Atwood Machine consists of two objects of mass m and M, connected by an inextensible massless string over an ideal massless pulley.

When $M=m$, the machine is in neutral equilibrium regardless of the position of the weights.

When $M \ne m$ both masses experience uniform acceleration.

Usefulness of Atwood Machine

1)The machine provides a way for students and scientists to confirm through demonstration and to better understand Newton’s second law of motion and other principles of physics and mechanics.

2) The two masses to be hung from the ends of the string, for example, will not move on their own as long as they are equal. Changing one of the masses so that they are not equal will result in one accelerating upward and the other downward, both at an equal and constant rate which does not change regardless of the size of either of the two masses.

3) A very large mass and a very small mass will both accelerate at the same constant rate as two masses that differ only slightly, and this machine allows this fact to be demonstrated under laboratory conditions.

Calculation  acceleration of the two masses

By applying Newton’s second law of motion, it can be calculated that when the two masses suspended by a string over a pulley are unequal, acceleration will result as the larger mass falls down and the smaller mass is pulled up and that this acceleration will be constant for both masses.

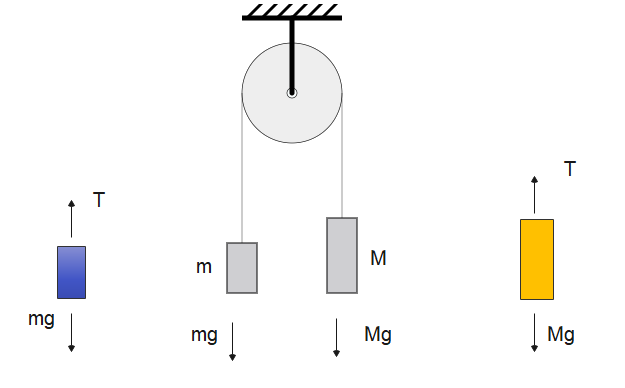
Draw good free-body diagram. Two, in fact, one for each mass.

Assume the pulley is frictionless and massless, which means the tension is the same everywhere in the string.
T1 = T2 = T
Analyze the system.It is clear that  If the system is released from rest, the heavy mass will accelerate down and the lighter one will accelerate up.

The  masses have the same acceleration, a.

Apply Newton’s second law for each mass. For mass M and  For mass m:

$Mg – T = Ma$

$T – mg = ma$

Combine the equations to eliminate T, so

$Mg – mg – ma = Ma$

or $a=\frac {(M-m)g}{(M+m)}$

We can analyze three cases based on above important derivation

i)If m = M then a = o. Makes sense – the system is balanced.
ii)If m = 0 then a = g. M is in freefall.
iii) If m > M then a is negative – the system goes the other way.

Solved Questions

Question 1

An Atwood machine consists of two masses, ( m_1 = 5 \, \text{kg} ) and ( m_2 = 3 \, \text{kg} ), connected by a string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string.

Solution

Now acceleration is given by

$a=\frac {(M-m)g}{(M+m)}$

$a= \frac {2 \times 10}{8} =2.5 \; m/s^2 $

Now, consider the force equation of mass 5 kg

$5 \times 10 – T = 5 \times 2.5$
or $T=37.5 N$

Question 2

A modified Atwood machine where ( m_1 = 4 \, \text{kg} ) is on a frictionless table connected by a string over a pulley to ( m_2 = 2 \, \text{kg} ) hanging vertically. Find the acceleration and the tension in the string

Solution

force equation for $m_1$

$m_1 g -T = m_1 a$

force equation for $m_2$

$T= m_2a$

so,

$a = \frac {m_1g}{m_1 + m_2} = \frac {40}{6} =3.67 \; m/s^2$

Now

$T= 2 \times 3.67= 7.2N$

I hope you like this article on Atwood machine

Related Articles

Mechanics of Turning a car on the curve
Free Body Diagrams
Newton’s Second Law Problems