We know that electric field inside a conductor is zero and any charge the conductor may carry shall be distributed on the surface of the conductor. The distribution of these surface charges depends on the shape of the conductor. For example, on a spherical conductor, the charge distribution is uniform, but it may vary on conductors of different shapes. we will check out now how to Electric field due to charged conductor
For our discussion consider a conductor carrying charge on its surface again consider a small surface element ds over which we can consider surface charge density $\sigma$ to be approximately constant.
For positive charge distributed over the surface of the conductor , electric field E would be directed at right angels to the surface pointing in outwards direction. Now E due to charge carrying conductor can be calculated using Gauss’s law. For this draw a Gaussin cylendrical surface as shown below in the figure
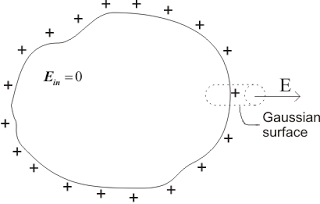
Now S is the area of cross-section of the surface. The flux due to cylendrical surface is zero because electric field and the normal to the surface are perpandicular to each other. Since electric field inside the conductor is zero hence only contribution to the flux is due to the chare on area S lying outside the surface of the conductor. So total flux through the surface would be
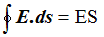
From Gauss’s law,
Gauss’s Law is crucial for understanding electric fields due to conductors. It states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space.
$E\cdot S=\frac {q}{\epsilon_{0}}=\frac{\sigma S}{\epsilon_{0}}$
or,
$E=\frac{\sigma}{\epsilon_{0}}$
and this is the required relation for the field of charged conductor
Important points
- For a conductor with a simple shape like a sphere, the above would be the uniform electric field near its surface
- For conductors with irregular shapes, the electric field is stronger where the curvature of the surface is greater. This is often why points or sharp edges of conductors have higher charge concentration and stronger electric fields.
- When a charged conductor is placed in an external electric field, the distribution of its surface charges adjusts such that the electric field inside the conductor remains zero.
In summary, the behavior of the electric field in and around a charged conductor is governed by the principles of electrostatics, particularly Gauss’s Law and the concept of electrostatic equilibrium. The exact nature of the electric field depends on the shape of the conductor, the distribution of charge on its surface, and the presence of any external electric fields.
I hope you like article on Electric field due to charged conductor. please do provide feedback
Related Articles
How to solve electric force and field problems
Force on a conductor in presence of an electric field
Electric charge and electric field questions and answers