we will check out Formula of frustum of cone in this post. we will also derive the formula so that it is easy to understand.
What is Frustum of cone
A frustum of cone is obtained by removing the upper part of the cone
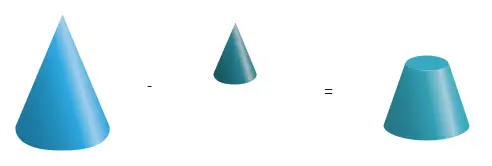
Lets take a look at the Frustum below
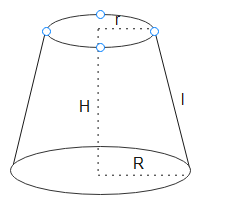
H is the height of the Frustum
R is the radius of the Base
r is the radius of the Top
l is the lateral height or slant height of the frustum
Formula for Volume of the Frustrum
$V = \frac {1}{3} \pi H(r^2 + R^2 + rR)$
Derivation
Lets take the full cone from where frustum is taken
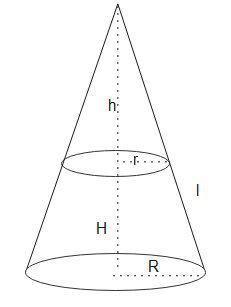
Volume of Frustum
$= \frac {1}{3} \pi (h+H)R^2 – \frac {1}{3} \pi h r^2$
Now from similar triangle theorem for right triangle for small clone and big close
$\frac {h}{h+H} = {r}{R}$
or $h = H \frac { r}{R-r}$
Substituting this in Volume
$= \frac {1}{3} \pi (H \frac { r}{R-r}+H)R^2 – \frac {1}{3} \pi H \frac { r}{R-r} r^2$
$=\frac {1}{3} \pi H ( \frac {R^3}{R-r} – \frac {r^3}{R-r})$
$= \frac {1}{3} \pi H \frac { R^3-r^3}{R-r}$
Now $a^3 -b^3 = (a-b) (a^2 + b^2 +a b)$
Therefore
$= \frac {1}{3} \pi H (r^2 + R^2 + rR)$
Formula for Curved Surface Area of the Frustrum
$S = \pi l ( r + R)$
where l is the slant height and it is given by
$l= \sqrt { H^2 + (R-r)^2}$
Derivation
Lets take the full cone from where frustum is taken
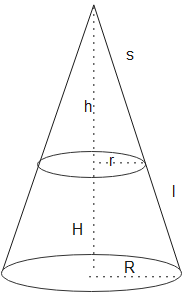
Curved surface area of frustum
$S= \pi R (s + l) – \pi r s$
Now from similar triangle theorem for right triangle for small clone and big close
$\frac {s}{s+l} = {r}{R}$
or $s = l \frac { r}{R-r}$
Therefore surface area is
$= \pi R (l \frac { r}{R-r} + l) – \pi r l \frac { r}{R-r} $
$= \pi l \frac {R^2}{R-r} – \pi l \frac {r^2}{R-r}$
$=\pi l \frac { R^2 -r^2}{R-r} = \pi l (R+r )$
Formula for Total Surface Area of the Frustrum
Formula for Total surface = Curved Surface Area + Area of Top + Area of base
$= \pi l (R+r ) + \pi (r^2 + R^2)$
Solved Examples
Question 1
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. Find the curved surface area of the bucket
Solution
Here l=45 cm, r=7 cm and R=28 cm
Curved Surface area= $\pi l(R+r) = \pi \times 45 (28 + 7) =\frac {22}{7} \times 45 \times 35 = 4950 cm^2$
I hope this article on Formula of frustum of cone helps you.
Related Articles
Class 10 Maths
Surface Area and Volume Class 10 Notes
 Skip to content
Skip to content