In this page we will explain the topics for the chapter 13 of Surface Area and Volume Class 10 Maths.We have given quality Introduction to Surface Area and Volume Class 10 Notes to explain various things so that students can benefits from it and learn maths in a fun and easy manner, Hope you like them and do not forget to like , social share
and comment at the end of the page.
Surface Area of Combination of Solids
- We saw different solids in our daily life
- These are not exactly the shape of single cube,cubiod,sphere,cylinder ,regular cone. They seems to be combination of these solids
- Let's take an example of solid below
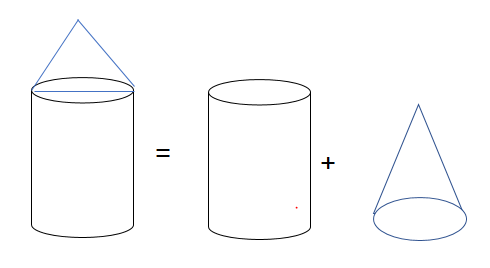
- So solids can be consider as combination of cylinder and Regular cone
- Surface area of the solid will be given
Surface Area of Solid = Curved Surface Area of Cylinder + Curved Surface area of Regular cone+ Surface area of cylinderical Base
$= 2\pi r h + \pi r L + \pi r^2$
- Similarly we can look at the below figure
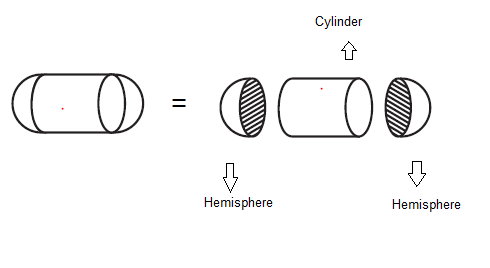
- Surface area of the solid will be given
Surface Area of Solid = Curved Surface Area of Cylinder + Curved Surface area of hemispshere+ Curved Surface area of hemispshere
$= 2\pi r2 h + 2 \pi r^2 + 2 \pi r^2$
Volume of Combination of Solids
- We discussed about surface area in the above section,let's see the volumen now.
- Let's take an example of solid below

- So solids can be consider as combination of cylinder and Regular cone
- Volume of the solid will be given
Volume of Solid = Volume of Cylinder + Volume of Regular cone
$= \pi r^2 H + \frac {1}{3} \pi r^2H $
- Similarly we can look at the below figure

- Volume of the solid will be given
Volume of Solid = Volume of Cylinder + Volume of hemispshere+ Volume of hemispshere
$= \pi r^2 h + \frac {2}{3} \pi r^3 + \frac {2}{3} \pi r^3$

Formula for Surface Area and Volume of Common Figures
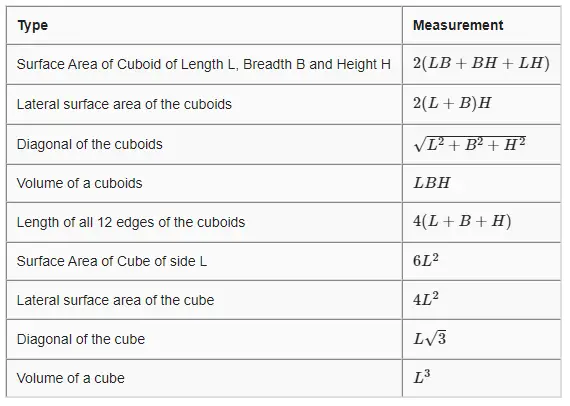
Surface Area and Volume of Cube and Cuboid<
Surface Area and Volume of Right circular cylinder

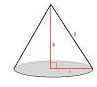
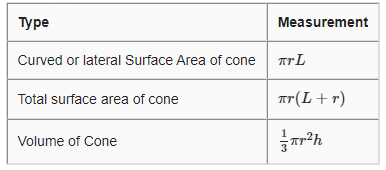
Surface Area and Volume of Right circular cone
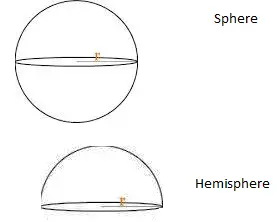
Surface Area and Volume of sphere and hemisphere

Surface Area and Volume of frustum of cone
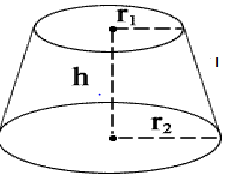
- Frustum of cone is created by removing some portion from top as shown above
- Here h = vertical height of the frustum
l = slant height of the frustum
$r_1$ and $r_2$ are radii of the two bases (ends) of the frustum.
How to solve Surface Area and Volume Problem of Combination of Solids
(1) We have explained the surface area and volume of various common sold shapes.
(2) We need to divide the given solid shape into known shapes
(3) Find out the given quantities like radius,height
(4) Apply the formula from the above given tables and get the answer
(5) Make sure you use common units across the problem
Question 1
The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm. Find its volume, the curved surface area and the total suface area?
Solutions
Here $h=45 \;cm ,r_1=7 \; cm ,r_2=28 \; cm$
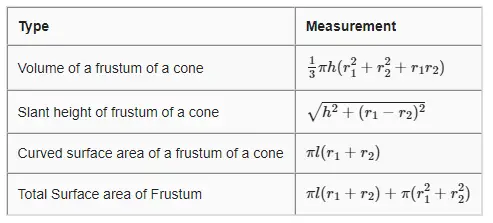
Volume of a frustum of a cone =$\frac {1}{3} \pi h(r_1^2 + r_2^2 + r_1r_2)$
$=48510 cm^3$
Since Curved surface area and Total Surface requires slant height,let's calculate that first
Slant height of frustum of a cone=$\sqrt {h^2 + (r_1 -r_2)^2}$
=49.65 cm
Now Curved surface area of a frustum of a cone=$ \pi l(r_1 + r_2)=5461.5 cm^2$
And Total curved surface area of the frustum =$ \pi l(r_1+ r_2) + \pi (r_1^2 + r_2^2)=8079.5 cm^2$
Question 2
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 4 cm and the diameter of the base is 8 cm. Determine the volume of the toy and the total surface area of the toy.
Solutions
Let r be the radius of the hemisphere and the cone and h be the height of the cone
r=4 cm and h=4 cm
Volume of the toy = Volume of the hemisphere + Volume of the cone
$= \frac {2}{3} \pi r^3 + \frac {1}{3} \pi r^2h$
$=\frac {1408}{7} cm^3$
total surface area of the toy=Curved surface area of cone + curved surface area of hemisphere
$=\pi rl +2 \pi r^2$
Now $l=\sqrt h^2 + r^2 =4 \sqrt 2$
So total surface area
$=171.68 cm^2$
Summary
Here is the Surface Area and Volume Class 10 Notes Summary
- We can find the surface area and volume of the various solid figures by dividing them into sphere, Cone, Cylinder, Cube, Cuboid and Frustum of the cone.
- When the smaller conical portion is removed from the top of the right circular cone, then the resulting solid formed is called a Frustum of a Right Circular Cone
- The volume of the frustrum is given by $V= \frac {1}{3} \pi h(r_1^2 + r_2^2 + r_1r_2)$
- The Total Surface area of the frustrum is given by $S= \pi l(r_1 + r_2) + \pi(r_1^2 + r_2^2)$
Also Read
- Notes
- Assignments
- NCERT Solutions












