Given below are the
Class 10 Maths Important Questions for Surface Area and Volume with Solutions
a. Frustrum problems
b. Melt and recasted problems
c. Hemisphere problems
d. Water pipe and tank problems
e. Mixture of shapes problems
Question 1. If the diameter of cross-section of a wire is decreased by 5% how much how much percent will be the length be increased so that the volume remains the same?
Solution
Original Volume=$\pi R^2 H$
When diameter is decreased by 5%, radius also is decreased by 5%.
New Radius = R - 5R/100 = 95R/100= 19R/20
New Volume=$\pi (\frac {19R}{20})^2 H = \frac {\pi \times H \times 361R^2}{400}$
But you want to maintain the volume at a constant, so Length H is to be multiplied by 400/361 to keep it constant.
So New Length= $ \frac {400H}{361}$
Increase in Length=$\frac {400H}{361 -H = \frac {39H}{361}$
% Increase in Length = $ \frac {39}{361} \times 100 = 10.8%$
Question 2. A solid sphere of radius 3cm is melted and then cast into small balls each of radius 0.3cm. Find the no. of balls thus obtained.
Solution
Let number of small balls = x
Volume of x small balls = Volume of sphere
$x \times \frac{4}{3}\pi (.3)^3 = \frac{4}{3} \pi (3)^3$
x=1000
Question 3. How many spherical bullets can be made out of a solid cube of lead whose edge measures 44cm, each bullet being 4cm in diameter?
Solution
Edge of the solid cube = 44 cm
Volume of the cube =L3= 443 = 85184 cm3
Diameter of the bullet = 4 cm
Radius = 2 cm
Volume of each bullet = $\frac {4}{3}\pi R^3$
= 33.5 cm3
Number of bullets = 85184 / 33.5 = 2542.8=2542(approx)
Question 4. A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?
Solution
Width 300cm=3m
depth 120cm=1.2m
speed of canal 20km/h= 20 * 1000m/h
vol. of water flow in 1 hour = width of canal �depth of canal * speef of canal water
=3 *1.2 * 20 * 1000=72000m3
So vol. of water flow in 20 min = 72000 * 20/60=24000m3
Area irrigated in 20 min =240000/0.08=300000m2
Question 5. A sphere of diameter 6cm is dropped in a right circular cylindrical vessel partly filled with. The diameter of the cylindrical vessel is 12cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Solution
Given
diameter of the sphere (d) = 6cm
�
radius of the sphere ( r ) = d/2 = 6/2 = 3cm
diameter of the cylindrical vessel ( D ) = 12 cm
radius of the cylindrical vessel ( R ) = 12/2 = 6 cm
Let level of water raised = h cm
Now according to the Question
volume of the water raised in the vessel = volume of the sphere
$
\pi R^2h = \frac {4}{3}�\pi r^3$
Substituting the values
h=1 cm
Question 6. A right circular cone is 3.6cm and the radius of its base is 1.6cm. It is melted and recast into a right circular cone with radius of its base as 1.2cm. Find its height.
Solution
For initial right circular core
h = 3.6 cm, r = 1.6 cm
Volume of the given cone =$ \frac {1}{3} \pi r^2 h = \frac {1}{3} \pi (1.6)^2 \times 3.6 cm^2$
For Final recast right circular cone
Radius of the second cone = 1.2 cm. Let its height be h
Volume of the second cone = $ \frac {1}{3} \pi r^2 h = \frac {1}{3} \pi (1.2)^2 \times h cm^2$
Now Volume of initial right circular core= Volume of Final recast right circular cone
$ \frac {1}{3} pi (1.6)^2 \times 3.6 =\frac {1}{3} pi (1.2)^2 \times h$
h=6.4 cm
Question 7. A conical vessel whose internal radius is 5cm and height 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10cm. Find the height to which the water rises.
Solution
Volume of water in conical vessel= $ \frac {1}{3} \pi r^2 h = \frac {1}{3} \pi (5)^2 24$
Let H be the height of water in cylinderical vessel.
Volume of water in cylinderical vessel=$ \pi r^2 h= \pi (10)^2 h$
Now Volume of water in conical vessel=Volume of water in cylinderical vessel
$\frac {1}{3} \pi (5)^2 24=\pi (10)^2 h$
h=2 cm
Question 8. Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube.Find the edge of the cube so formed
Solution
$l= (3^3 + 4^3 + 5^3)^{1/3} = 6$
Question 9. Find the number of coins, 1.5cm in diameter and 0.2cm thick, to be melted to form a right circular cylinder of height 10cm and diameter 4.5cm.
Solution
Each one of those coins is also a small cylinder , and its volume is�
$
V_1 = \pi r^2h = \pi (.75)^2(.2)$
�
The right circular cylinder has volume $
$V_2 = \pi r^2 h=\pi (2.25)^2(10)$�
Number of Coins =$\frac {V_2}{V_1} = 450$ coins�
Question 10. A glass cylinder with diameter 20cm has water to a height of 9cm. A metal cube of 8cm in emerged in it completely. Calculate the height by which water will rise in the cylinder.
Solution
Let h be the height water rise in cylinder
So Volume of the portion of increase in height = $\pi (10)^2 h$
Volume of cube=$ (8)^3$
Now Volume of cube= Volume of the portion of increase in height
$(8)^3=\pi (10)^2 h$
h=1.62 cm
Question 11. A well, whose diameter is 7cm, has been dug 22.5m deep and the earth dugout is used to form an embankment around it. If the height of the embankment is 1.5m, find the width of the embankment.
Solution
Let x be the width
Volume of well=$\pi r^2 h= \pi \times (3.5)^2 \times 22.5 $
Volume of embankment=$ \pi R^2 h - \pi r^2 h=\pi \times (3.5 +x )^2 \times 1.5 - \pi \times (3.5)^2 \times 1.5$
Volume of well = Volume of embankment
So $\pi \times (3.5)^2 \times 22.5 = \pi \times (3.5 +x )^2 \times 1.5 - \pi \times (3.5)^2 \times 1.5$
On solving we get x = 10.5m
Question 12.An agriculture field is in the form of a rectangle of length 20m and width 14m. A 10m deep well of diameter 7m is dug in a corner of the field and the earth taken out of the well is spread evenly over the remaining part of the field. Find the rise in the level.
Solution
Volume of deep well= $\pi r^2 h = \pi \times (3.5)^2 \times 10$
Let h be the rise in level
Volume of earth spread out = $20 \times 14 \times h$
Now,
Volume of earth spread out=Volume of deep well
$\pi \times (3.5)^2 \times 10=20 \times 14 \times h$
h=11/8 m
Question 13. The perimeters of ends of a frustum are 48cm & 36cm, if height of frustum be 11cm, find its volume.
Solution
Volume of a frustum of a cone =$\frac {1}{3} \pi h(r_1^2 + r_2^2 + r_1r_2)$
Here h=11 cm , $r_2= \frac {48}{2 \pi}=\frac {24}{\pi}$ , $r_1 =frac {36}{2 \pi}=\frac {18}{\pi}$
Substituting these values
V=1554 cm3
Question 14. A cylindrical pipe has inner diameter of 7cm and water flows through it at 192.5 l/min. Find the rate of flow in kilometers per hour.
Solution
Radius of cylindrical pipe = 7/2 cm
=3.5 cm
Volume of water flows in 1 min = 192.5 L
Therefore,Volume of water flows in 1 hour = $192.5 \times 60 \times 1000 cm^3$
Let l be the distance covered by water in 1 hour.
Volume of water that covers the diameter of 1 hour =volume of cylinder per hour=$ \pi \times r^2 \times l=\pi \times (3.5)^2 \times l cm^3$
Now
$ \pi \times (3.5)^2 \times l=192.5 \times 60 \times 1000 $
l=300000 cm= 3km
So rate of flow is 3km/hr
Question 15. Water is being pumped out through a circular pipe whose internal diameter is 7cm. if the flow of water is 72cm per second, how many liters of water are being pumped out in one hour?
Solution
Radius of circular pipe (r) = 7/2 =3.5cm
Now
Length of water per sec = 72cm
Therefore, volume of water per second = volume of cylinder per second
=$ \pi r^2 h = \frac {22}{7} \times (3.5)^2 \times 72
= 2772 cm^3$
Now $
1 L = 1000cm^3
$
So, volume of water per sec = 2.772 litres
Hence volume of water in hr= $2.772 \times 60=9979.2 litres$
Question 16. Water is flowing at the rate of 3km/hr through a circular pipe of 20cm internal into a circular cistern of diameter 10m and depth 2m.In how much time will cistern will be filled?
Solution
Radius of pipe(r) = 20/2 cm = 10 cm = 1/10 m
Height of water in 1 hour(
h)= 3 km = 3000 m
Volume of water passing through the pipe in a hour
= Volume of the cylinder formed
$V = \pi r^2 h= \pi \times (1/10)^2 \times 3000 = 30 \pi$
Volume of cistern
$V = \pi r^2 h=\pi \times (5)^2 \times 2=50 \pi$
Therefore time needed to fill the cistern =$ \frac {50 \pi}{30 \pi} = \frac {5}{3}$ hr
Question 17. Water is flowing at the rate of 7 meters per second through a circular pipe whose internal diameter is 2cm into a cylindrical tank the radius of whose base is 40 cm determine the increase in the water level in ½ hours.
Solution
Volume of water in 1/2 hours= $ \pi \times (1)^2 \times 700 \times 30 \times 60$
Let H be the increase in the water level
Then
$\pi \times (40)^2 \times H=\pi \times (1)^2 \times 700 \times 30 \times 60$
H=787.5cm
Question 18. An inverted cone of vertical height 12cm and radius of the base 9cm has water to a depth of 4cm.Find the area of the internal surface of the cone not in contact with water
Solution
The situation is shown in below figure
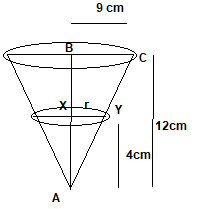
By similarity of triangle ABC and AXY
$\frac {AB}{AX} = \frac {BC}{XY}$
$\frac {12}{4}=\frac {9}{r}$
r=3 cm
The area of the internal surface of the cone not in contact with water is the area of the frustum of the cone which is given as
$A =\pi L(r_1+ r_2)$
Here $r_1=3 cm $ ,$r_2= 9 cm$
Also height of the frustum = 12 -4 =8 cm
Now L is given by
$L= \sqrt {h^2 + (r_2 -r_1)^2} =10$ cm
Therefore Area
$A= \frac {22}{7} \times 10 ( 3 + 9) = 376.8 cm^2$
Water is flowing at the rate of 5km /hr through a pipe of diameter 14m into a rectangular tank which is 50m long and 44m wide. Determine the time in which the level of water in the tank will rise by 7cm?
Solution
Answer 2.5cm
Question 20. Water in a canal, 30dm wide and 12dm deep is flowing with velocity of 10km/hr. How much area will it irrigate in30minutes if 8cm of standing water is required for irrigation?
Solution
Answer 225000m2
Question 21. Water flow at the rate of 10 meters per minute through a cylindrical pipe having the diameter as 5mm. How much time will it take to fill a conical vessel whose diameter of base is 40cm and depth24cm?
Solution
Answer 51 minutes 12 seconds
Question 22. A hemispherical tank of radius 1.75m is full of water. It is connected with a pipe which empties it at the rate of 7 litres per second. How much time will it take to empty the tank completely?
Solution
Answer 26.73 minutes
Question 23. The barrel of a fountain pen, cylindrical in shape, is 7cm long and 5mm in diameter. A full barrel of ink in the pen will be used upon writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
Solution
Radius of the barrel=5/2 = 2.5mm= .25 cm
Height of bareel= 7 cm
Volume of the barrel= $\pi r^2 H= $ \frac {22}{7} \times (.25)^2 \times 7=1.375 cm^3$
Now 1/5 litre means = $200 cm^3$
Now as per the question
$1.375 cm^3$ of ink can write 3300 words
$1 cm^3$ of ink will write $\frac {3300}{1.375}$ words
$200 cm^3$ will write $\frac {3300}{1.375} \times 200=480000$ words
Question 24. The cost of painting the total outside surface of a closed cylindrical oil tank at 60 paise per sq. dm is Rs. 237.60. The height of the tank is 6 times the radius of the base of the tank. Find its volume correct to two decimal places.
Solution
Answer 509.14dm3
Question 25. A solid iron rectangular block of dimensions 4.4 m, 2.6m, and 1m is cast into a hollow cylindrical pipe of internal radius 30cm and thickness 5cm. Find the length of the pipe. (Use Π = 22/7)
Solution
Volume of the solid iron rectangular block= $4.4 \times 2.6 \times 1=11.44 m^3$
Internal Radius(r)=30 cm
External radius(R) = 30 +5=35 cm
Let L be the lenght of the pipe,Then volume of the pipe will be
$V=\pi R^2 L - \pi r^2 L = \pi L[(.35)^2 - (.30)^2]$
Now As per the question
Volume of the solid iron rectangular block=volume of the pipe
$11.44=\pi L[(.35)^2 - (.30)^2]$
L=112m
Question 26.
A building is in the form of a cylinder surmounted by a hemispherical dome . The base diameter of the dome is equal to 2/3 of the total height of
the building. Find the height of the building, if it contains $67 \frac {1}{27} m^3$ of air
Solution
Let the radius of the hemispherical dome be r metres and the total height of the building be h metres.
Since the base diameter of the dome is equal to 2/3 of the total height, therefore
$2r = \frac {2}{3} h$. This implies $r = \frac {h}{3}$
Let H metres be the height of the cylindrical portion.
Therefore, $H =h � \frac {h}{3} = \frac {2h}{3}$ m
Volume of the air inside the building = Volume of air inside the dome + Volume of the air inside the cylinder
$V= \frac {2}{3} \pi r^3 + \pi r^2 H$
Substituting the value of r and H, we get
$=\frac {8}{81} \pi h^3$
Now as per the question
$\frac {8}{81} \pi h^3=67 \frac {1}{27}$
or h=6 m
Summary
This Class 10 Maths Important Questions for Surface Area and Volume with answers is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail.
link to this page by copying the following text
Also Read
- Notes
- Assignments
- NCERT Solutions
