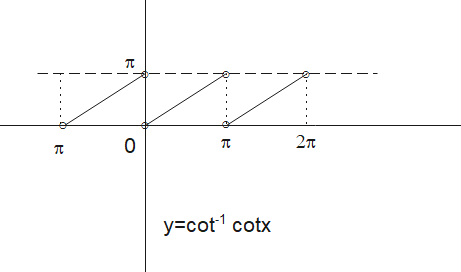Here in this post ,we will check out how to draw the graph of cot inverse cot x i.e
$f(x) = cot^{-1} cot (x)$
As $cot (\pi +x ) = cot x$
This is a periodic function with period $\pi$
Also x cannot take values like $n \pi$ as undefined
We know by definition
$f(x) = cot^{-1} cot (x) = x $ if $x \in (0, \pi)$
Lets check out the other values
if $x \in (-\pi, 0)$
$-\pi < x < 0 $
Adding $\pi$
$0 < x < \pi $
Also $cot( \pi +x) = cot x$
So $f(x) = cot^{-1} cot (x) = cot^{-1} cot (\pi +x )= \pi + x $
if $x \in (\pi, 2 \pi)$
$\pi < x < 2\pi $
subtracting $\pi$
$0 < x -\pi < \pi $
Also $cot( \pi -x) = -cot x$
or $cot( x- \pi) = cot x$
So $f(x) = cot^{-1} cot (x) = cot^{-1} cot (x – \pi )= x – \pi $
Therefore the graph will be