how to prove one-one functions with examples

This post we will see given a function, how to check if it is one-one function or not. Lets first start with the definition of the one-one functions

Definition of one-one functions

A function f: A-> B is said to be one-one

if, and only if, for all elements a₁ and a₂ in A,

if f(a₁) = f(a₂), then a₁ = a₂

how to prove one-one function

To prove that a function is one-to-one (also known as injective), you need to show that no two distinct inputs have the same output. Here’s the general method for proving that a function f: A -> B is one-to-one:

Method 1

1. Assume that $f(x_1) = f(x_2)$ for some x1 and x2 in the domain A.
2. Use this assumption to show that $x_1 = x_2$.For example, you might start by assuming that f(x1) = f(x2), and then subtracting one equation from the other:f(x1) – f(x2) = 0 and then proving it

Example

f: R -> R given as f(x) = 2x +3

So,

$f(x_1)=f(x_2)$
$2x_1 +3= 2x_2 +3$
or

$x_1=x_2$

Conclude that the function is one-to-one. Since you have shown that no two distinct inputs have the same output, you can conclude that the function is one-to-one

Method 2

If you know the graph or you can draw the graph easily, then you can use Horizontal line test to determine if it is one-one function or not

if a horizontal line intersects the graph at two points then it is not an one-one function. This is called the Horizontal line test. If all horizontal lines intersect a curve at most once then the curve represents a one-one function.

Example

The graph of the function f:R ->R f(x)=x(4-x) as

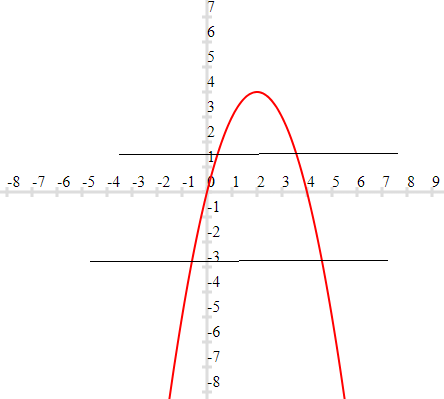
So this is not one-one function

Method 3

Take counter examples

Example Let function f : R -> R, defined as $f(x) = x^2$

Solution

We can try to counter examples to check

here we can see that f(1) =1 ,f(-1) =1

Hence it is not a one-one function

Method 4

Strictly increasing or decreasing functions are one-one

for f(x) if $\frac {d f(x)}{dx} > 0$, Then f(x) is strictly increasing. So we can find the derivative and then determine if it is one-one or not
for f(x) if $\frac {d f(x)}{dx} < 0$, Then f(x) is strictly decreasing. So we can find the derivative and then determine if it is one-one or not

Example

Let f:[2,$\infty$) -> R, $f(x)=x^3 -2x^2 +1$

$\frac {d f(x)}{dx} = 3x^2 -4x= x(3x-4) > 0 , x> 2$

Hence f(x) is one -one function

Solved Examples

Example 1

f: R -> R such that $f(x)=\frac {x}{x^2 + 1}$. Check if this one-one

Solution

$f(x_1)=f(x_2)$

$\frac {x_1}{x_1^2 + 1}=\frac {x_2}{x_2^2 + 1}$

$(x_2 -x_1)(x_1 x_2 -1)=0$

So either $x_1=x_2$
or
$x_1 x_2 =1$
here since x belongs to R, we can have $x_1=2$ and $x_2=1/2$ as values satisfying this

Also f(2)=2/5
and f(1/2)=2/5

Hence this is not one-one functions