This post we will see given a function, how to check if it is onto function or not. Lets first start with the definition of the onto functions
Definition of onto functions
A function f: A-> B is said to be onto(surjective) if every element of B is the image of some element of A under f, i,e for every $y \in B$, there exists a element x in A where f(x)=y
how to prove onto function
To prove that a function is onto, also known as surjective, you need to show that every element in the range of the function has at least one preimage in the domain. In other words, there are no elements in the range that are not mapped to by at least one element in the domain.
Method I
we take any element y in the range of function and then try to see if there exists an element in the domain of f such that f(x) = y
Example: Let f: R-> R be defined by f(x) = 3x – 2. Prove that f is onto.
Solution: To prove that f is onto, we need to show that every element y in the range of f has at least one preimage x in the domain of f such that f(x) = y.
Let y be an arbitrary element in the range of f, that is, $y \in R$. We need to find an element x in the domain of f such that f(x) = y.
Setting y = 3x – 2, we can solve for x as follows:
y + 2 = 3x
x = (y + 2)/3
Also it follows
f((y+2)/3 )= 3(y+2)/3 -2=y
So we have found an expression for x in terms of y. Also we see that y can take any value in R and x will belong to R for any value of Y. This means that for any element y in the range of f, there exists an element x in the domain of f such that f(x) = y.
Therefore, we have shown that f is onto, and our proof is complete.
Note that in this example, we used an arbitrary element y in the range of f to find a corresponding preimage x in the domain of f. This is a general strategy for proving that a function is onto.
Method 2
Take counter examples
Example Let function f : R -> R, defined as $f(x) = x^2$
Solution
We can try to counter examples to check
here we can see there exists no real number for y=-4
$-4=x^2$
Hence it is not a onto function
Method 3
We can draw the graph of the function and if it is covering all the values of y, then it is onto function
Example Let function f : R -> R, defined as $f(x) = |x|$
Solution
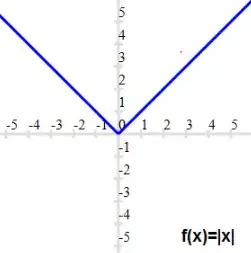
We can see that it is not covering all the values of y ,so it is not onto function
Solved Examples
Example 1
Let A ={1,2,3}
and function F on A is defined as ={(1,1), (2,2) , (3,3)}
Find out if it is onto
Solution
we can see that f(1)=1 , f(2)=2 and f(3)=3
So all elements in A has a pre image, so it is onto function
Example 2
Let f : R -> R
f(x) =x |x|
Find out if it is onto
Solution
To determine whether the function f(x) = x|x| is onto, we need to show that for every y in the range of f, there exists at least one x in the domain of f such that f(x) = y.
Case 1
x is positive or zero In this case, we have $y = x|x| = x^2$ .
Therefore, $x = \sqrt {y}$
So we will have preimage for all positive values of y
Case 2
x is negative In this case, we have y = x|x| = -x^2 . Therefore, we can take $x = – \sqrt {|y|}$
So we will have preimage for all negative values of y
Therefore, f is onto.
Therefore, the function f(x) = x|x| is onto, and we have shown this by finding at least one preimage for every element in the range.
Example 3
if f: R -> R where $f(x)= \frac {x^2 + 3x+6}{x^2 +x + 1}$. check if this is onto
Solution
$f(x)= \frac {x^2 + 3x+6}{x^2 +x + 1} = \frac { (x+ 3/2)^2 + 15/4}{(x+ 1/2)^2 + 3/4}$
So this means f(x) only takes positive values.
So this is not onto function
Related Articles
