What is the most basic formula to calculate acceleration?

The most basic formula for acceleration is a = (v - u)/t, where 'a' is acceleration, 'v' is final velocity, 'u' is initial velocity, and 't' is the time taken. This formula shows how quickly velocity changes over time.

How do you find acceleration when only velocity and distance are given?

When you have velocities and distance but not time, use the kinematic equation a = (v² - u²)/2s, where 'v' is final velocity, 'u' is initial velocity, and 's' is the distance traveled.

What does negative acceleration indicate in physics?

Negative acceleration indicates deceleration or retardation, meaning the object is slowing down. It occurs when the acceleration vector points in the opposite direction to the velocity vector.

What are the correct units for acceleration?

The standard SI unit for acceleration is meters per second squared (m/s²). This represents how much the velocity (in m/s) changes each second.

How do you choose which acceleration formula to use?

Choose a = (v - u)/t when you know initial velocity, final velocity, and time. Use a = (v² - u²)/2s when you know initial velocity, final velocity, and distance. The choice depends on which quantities are given in the problem.

How to solve for acceleration in physics?

Acceleration ($a$) is defined as the rate of change of velocity. It tells you how quickly velocity increases or decreases.

The question ‘How do you solve for acceleration in physics?’ can be answered briefly as follows:

Acceleration is calculated by $ a=\frac{v – u}{t}$, where $u$ is initial velocity, $v$ is final velocity, and $t$ is time; if distance is given, use $a = \frac{v^2 – u^2}{2s}$.
Tweet

Here, I’ve introduced two formulas—we’ll go through each one step by step, along with a solved example for better understanding.

How to solve for acceleration in physics

Using basic formula for acceleration

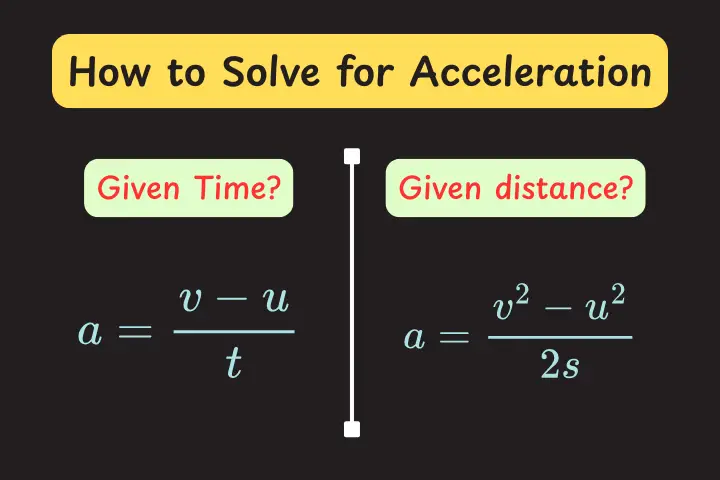
$$a = \frac{v – u}{t}$$

This is the most commonly used formula to find acceleration when initial velocity ($u$), final velocity ($v$) and time ($t$) are given.

Where:

$v$ = final velocity
$u$ = initial velocity
$t$ = time taken

Steps to solve for acceleration

(1) Identify given quantities

Look for values of initial velocity ($u$), final velocity ($v$), and time ($t$). Units must be consistent (m/s for velocity, s for time).

(2) Choose the right formula

Use

$$
a = \frac{v – u}{t}
$$

when you know $u$, $v$ and $t$.

(3) Plug in the values

Substitute the known values carefully.

(4) Solve and include units

Write final acceleration with units (usually $m/s^2$).

Example:
A car increases its speed from 10 m/s to 30 m/s in 5 seconds. Find its acceleration.

Given:

$u = 10, m/s$
$v = 30, m/s$
$t = 5, s$

Putting the values in the formula:

$$
a = \frac{v – u}{t} = \frac{30 – 10}{5} = \frac{20}{5} = 4\, m/s^2
$$

So, the car accelerates at $4, m/s^2$.

Other situations: using equations of motion

This formula is used when you don’t have time but have distance ($s$) over which the velocity changes.

$$
v^2 = u^2 + 2as
$$

Rearrange to solve for $a$:

$$
a = \frac{v^2 – u^2}{2s}
$$

Example:
A bike slows down from 20 m/s to 10 m/s over a distance of 50 m. Find its acceleration.

Given:

$u = 20, m/s$
$v = 10, m/s$
$s = 50, m$

Putting the values:

$$
a = \frac{v^2 – u^2}{2s} = \frac{(10)^2 – (20)^2}{2 \times 50} = \frac{100 – 400}{100} = \frac{-300}{100} = -3\, m/s^2
$$

Here, the negative sign indicates deceleration, meaning the bike is slowing down.

Summary Table

Known quantities	Use formula
$u, v, t$	$a = \frac{v-u}{t}$
$u, v, s$	$a = \frac{v^2-u^2}{2s}$
$u, a, t$ to find $v$	$v = u + at$
$u, a, s$ to find $v$	$v^2 = u^2 + 2as$

Conclusion

So whenever you get a problem on acceleration, first look at what quantities are given — velocity and time, or velocity and distance. Then simply pick the right formula:

Use $\displaystyle a = \frac{v – u}{t}$ if time is given.
Use $\displaystyle a = \frac{v^2 – u^2}{2s}$ if distance is given.

With this method, solving for acceleration becomes very straightforward.