

Welcome to this collection of Class 9 Physics Chapter 7 – Motion numericals with answers. This page includes solved numerical problems based on the NCERT syllabus, covering key topics like equations of motion, acceleration, uniform and non-uniform motion, and circular motion. A PDF worksheet is also available for download. These motion numerical questions are designed to help CBSE and ICSE students practice, revise, and score better in exams.
a. Acceleration is given by
\(a = \frac{{\Delta v}}{{\Delta t}}\)
$\Delta v = 54 -36 = 18 km/hr =\frac {18 \times 1000}{3600} m/s= 5 m/s$
So a=.5 m/s2
b. Distance is given by
\(S = ut + \frac{1}{2}a{t^2}\)
Now u=36 km/hr =10m/s
$s=10 \times 10 + \frac {1}{2} \times .5 \times 10^2$
So s=125m
might be accelerated
Here u=54 km/h =15 m/s ,v=36 km/h=10 m/s
Acceleration is given by
\(a = \frac{{\Delta v}}{{\Delta t}}\)
$a = \frac {10 -15}{10} =- .5$
So a=-.5 m/s2
Negative sign implies retardation
| S.no | Rounds | Displacement | Distance |
|---|---|---|---|
| 1 | 1 | ||
| 2 | 1.5 | ||
| 3 | 2 | ||
| 4 | 2.5 |
After every round, particle comes to it starting position. So displacement at full rounds will be zero
| S.no | Rounds | Displacement | Distance |
|---|---|---|---|
| 1 | 1 | 0 | \(20\pi \) |
| 2 | 1.5 | 20 m | \(30\pi \) |
| 3 | 2 | 0 | \(40\pi \) |
| 4 | 2.5 | 20m | \(50\pi \) |
Acceleration is given by
\(a = \frac{{\Delta v}}{{\Delta t}}\)
$ a = \frac {20 -10}{4} = \frac {10}{4}=2.5$
So a=2.5 m/s2

Here u=0 ,a= 5m/s2 ,t= 5 sec,v=?
Now $ v=u+at$
$v= 0 + 5 \times 5 =25$ m/s
Answer is (c)
$ \text {Average speed}= \frac {\text {total distance}}{time} =\frac {500}{10}=50$ km/hr
Ratio of average speed to maximum speed= 50:90=5:9
u=0, v=54 km/h=15 m/s ,t=2 sec
a) Acceleration is given by
\(a = \frac{{\Delta v}}{{\Delta t}}\)
$a = \frac {15-0}{2}$
So a=7.5 m/s2
b) Distance is given by
\(S = ut + \frac{1}{2}a{t^2}\)
$s= 0 \times 2 + \frac{1}{2} \times 7.5 \times 4$
s=15m
$v=u+at$
\(u = 0\)
\(v = 10 \times 5 = 50m/s\)
As it comes down to the initial point
Net displacement is zero
Net distance=200 m
We know that
$Distance = speed \times time$
Distance travelled in first 2 minute = $\frac {7.5 \times 2}{60}$ = 0.25 km
Distance travelled in last 2 minute = $\frac {7.5 \times 2}{60}$= 0.25 km
Total distance = .25+.25 = 0.5 km
Total time = 2+2+56 = 60 minute = 1 hr
Average speed = 0.5/1
= 0.5 km/hr
$speed =\frac {distance}{time}$
or
$time= \frac {distance}{speed}$
For travelling 1 km with 3 km/hr,
Time taken = 1/3 hr = 20 min
Now he has to reach school in 30 min,So he has cover another 1 km in = 30 -20 =10 min= 1/6 hr
So speed should = distance /time= 1/(1/6) = 6 km/hr
u=10 m/s,t=2 s, a=2 m/s2
$v=u+at$
$v= 10 + 2 \times 2 =14$ m/s
We are given the following information:
Initial velocity, \(u = 20 \, \text{m/s}\)
Distance traveled, \(d = 6 \, \text{cm} = 0.06 \, \text{m}\)
We can use the equation of motion:
\[v^2 = u^2 + 2ad\]
Since the bullet comes to rest (\(v = 0 \, \text{m/s}\)), we have:
\[0 = u^2 + 2ad\]
Solving for deceleration (\(a\)):
\[2ad = -u^2\]
\[a = \frac{{-u^2}}{{2d}}\]
Substituting the given values:
\[a = \frac{{-(20 \, \text{m/s})^2}}{{2 \cdot 0.06 \, \text{m}}}\]
\[a = -\frac{{400 \, \text{m}^2/\text{s}^2}}{{0.12 \, \text{m}}}\]
\[a = -3333.33 \, \text{m/s}^2 \, \text{(rounded to two decimal places)}\]
Therefore, the deceleration of the bullet in the sand box is approximately \(-3333.33 \, \text{m/s}^2\).
(c)
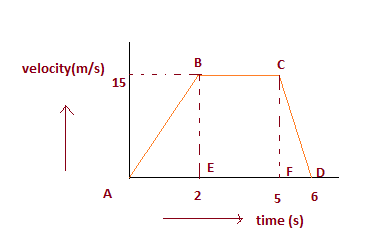
a. The distance travelled by the SUV is first 2 seconds = Area of $\Delta ABE$
$= \frac {1}{2} \times AE \times BE$
$=\frac {1}{2} \times 2 \times 15= 15m$
b. Acceleration will be given by the slope of the line CD
$a= \frac {0 -15}{6-5} = -15 m/s^2$
Now mass of the SUV =1000 Kg
Braking Force will be
$F=ma = 1000 \times -15 =-15000 N$
Given $u= 5 \times 10^3 m/s$ , $a=10^3 m/s^2$, $v=2u =10^4$ m/s
i.Using $v=u+at$
$10^4 = 5 \times 10^3 + 10^3 t$
or
t=5 sec
ii. Using $s=ut+ \frac {1}{2}at^2$
$s = 5 \times 10^3 \times 5 + \frac {1}{2} \times 10^3 \times 5^2$
$=37.5 \times 10^3 m$
Given Lenght of Train = 100m , velocity = 72 km/hr = 20 m/s, Lenght of the Bridge =2 Km.
Total distance covered by the train to fully pass the bridge = 2000 + 100 = 2100 m
So, time taken
$ time = \frac {distance}{velocity} = \frac {2100}{20} =105 sec$
Given r =42.250 km , T= 24 hour
Linear velocity in circular motion is given by
$v = \frac {2 \pi r}{T} = \frac {2 \times 3.14 \times 42.250}{24} = 11.05 km/hr$
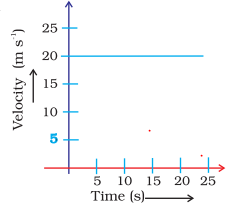
(i) We can see from the graph that velocity is not changing So,acceleration is equal to zero.
(ii) By Reading the graph, velocity = 20 m/s
(iii) Distance covered in 15 seconds, $s = u \times t = 20 \times 15 = 300$ m
Here u=0, s=20 m ,t=2 sec
\(S = ut + \frac{1}{2}a{t^2}\)
$20= 0 + \frac {1}{2} a \times 4$
$a=10 m/s^2$
Now Velocity at the end of 2 sec
$v=u+at$
$v=10 \times 2=20$ m/s
Now Checking the motion for next 4 sec, let assume acceleration be $a_1$ as we are not sure about the motion in second part
Here u=20 m/s ,s=160 m ,t=4 sec
\(S = ut + \frac{1}{2}a{t^2}\)
$160 = 20 \times 4 + \frac {1}{2} a_1 \times 16 $
$a_1 = 10 m/s^2$
So acceleration is constant in both the motion.
Now we can easily calculate velocity as
u=0, t= 7sec , a=10m/s2
$v=u+at$
$v= 0 + 10 \times 7= 70 m/s$
Total distance travelled by the object =20 m + 16 m = 36 m
Total time taken = 2 s + 2 s = 4 s
$\text {Average Speed} = \frac {\text {total Distance travelled}}{\text {total time taken }}$
$\text {Average Speed} = \frac {36}{4} = 9$ m/s
(d) only.
Distance and displacement in all other cases
Here u=72 km/hr = $\frac {72 \times 1000}{3600} m/s= 20$ m/s , v=0
a= -5 m/s2
Now using the relation
$v^2 = u^2 + 2as$
$0 = (20)^2 + 2 \times (-5) \times s$
$s= 40 m$
This numericals of motion class 9 with answers is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail. You can download this as PDF also
Download Numerical Motion Problems and Solution worksheet as pdf