How to solve Simple Harmonic Motion(SHM) problems effectively for JEE Main/Advanced

What is Periodic Motion

In Physics, a motion that is regular and repeating is called Periodic Motion. The time to complete one full motion is called the Time period of the Periodic Motion

What is SHM:

A Simple Harmonic Motion is a special case of Periodic motion where a physical quantity varies sinusoidal. In this Periodic motion the restoring force is directly proportional to the displacement. The object oscillates between two position and Motion is sinusoidal in nature.

Mathematically it is expressed as
$m\frac{d^{2}x}{dt^{2}}=-kx$
The above equation is called the equation for Simple Harmonic Oscillator.
The equation above can be written as
$\frac{d^{2}x}{dt^{2}}=-(k/m) x$

The constant (k/m) is called the proportinality constant.

The general solution for this equation is
$x=Asin\omega t+Bcos\omega t$
Where
$\omega =\sqrt{\frac{k}{m}}$
The A and B constant can be calculated based on the values given for initial conditions.

Linear SHM and Angular SHM

Linear Simple Harmonic Motion when the object is oscillating along straight line.The restoring force should be proportional to the displacement from the mean position and acting towards means position

Angular Simple Harmonic Motion when the object is oscillating along circular arc. The restoring torque acting on the object is proportional to angular displacement from mean position and direction of torque is always in such a way that it will try to bring the object to the equilibrium position

How to Solve the Simple Harmonic Motion problems

There are two ways in which the problem can be solved.
1) Force method or Torque Method: You will need to calculate all the forces or torque acting the object and then try to derive the SHM general equation

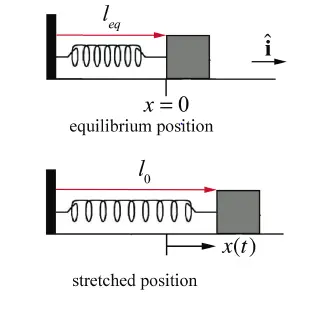
How to solve the SHM problem using Force method
1) Read the situation carefully to fully understand.
2) Displace the object from equilibrium position
3) Find all the forces or torque acting on the object in displaced position
4) Establish a relationship between restoring force and displacement.
5) Derive the angular frequency using the standard relation
Example:
Let us a take spring mass system

A body of mass m is attached to the spring of spring constant k. The body is displaced by some position and then left .Lets us find the force acting on the body at some point t and position x
The force acting on the body is the restoring force of the spring giving by kx,so
F=-kx
or
$m\frac{d^{2}x}{dt^{2}}=-kx$
$\frac{d^{2}x}{dt^{2}}=-(k/m) x$

2) Energy Approach: You will need to find all the energy and then differentiate with respect to time
i.e
$\frac{dE}{dt}=0$
Example : Take the abov example only
Total energy at any point t( It will consists of energy stored in spring + Kinetic energy of the object)
$E=\frac{1}{2}mv^{2}+\frac{1}{2}kx^{2}$
Differentiating wrt to time on both sides
$\frac{dE}{dt}=mv\frac{dv}{dt}+kx\frac{dx}{dt}$
$0=v(m\frac{d^{2}x}{dt^{2}}+kx)$
or
$\frac{d^{2}x}{dt^{2}}=-(k/m) x$

Energy method is much better in case of Complex system as it is easy to find the energy
How to solve the SHM problem using Energy method
1) Read the sutuation carefully to fully understand.
2) Check all the energy components of the system at any time t.
3) Add all the energy components and we need to make sure we can expressess all the individual terms in same physical quatities. We can make use of different physical formulas to do it. Like angular velocity can be expresses in linear velocity using $v=r\omega$
4) Differentiate with respect to time on both side and put (dE/dt=0) and solve it to find the general SHM motion equation

Example :

A sold cylinder of Mass M and Radius R is atached to the spring of spring constant K as shown in figure above.It rolls without slipping on the horizontal floor. The cylinder is move away from the equlibrium position and then left. Let us take a time t, the spring is stretched by x and Center of mass of the cylinder is moving with velocity v

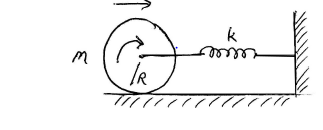
Let us take a look at the energy in the system
1) Spring Potential energy given by (1/2)kx²
2) Cylinder Kinetic energy given by (1/2)Mv²
3) Cylinder Rotational energy give by $(1/2)I\omega^{2}$
Where I is moment of Inertia and $\omega$ is the angular velocity of the cylinder about center of mass
Now I=(1/2)MR² and as the cylinder is rolling without slipping $\omega=v/R$
So cylinder Rotational energy becomes
1/4)MR²(v/R)²
=(1/4)Mv²
Now Total energy
$E=\frac{1}{2}Mv^{2}+\frac{1}{2}Kx^{2}+\frac{1}{4}Mv^{2}$
Now
Differentiating both sides and putting dE/dt=0, we get

$\frac{d^{2}x}{dt^{2}}=-(2K/3M) x$
Thus angular frequency of the SHM is
$\omega =\sqrt{\frac{2K}{3M}}$

Time period and Angular Frequency for Common SHM scenario

Spring Mass System

$\omega =\sqrt{\frac{k}{m}}$

$Time-period(T) =2 \pi \sqrt{\frac{m}{k}}$

Simple pendulum

$\omega =\sqrt{\frac{g}{l}}$

$Time-period(T) =2 \pi \sqrt{\frac{l}{g}}$

Compound Pendulum

$\omega =\sqrt{\frac{mgl}{I}}$

$Time-period(T) =2 \pi \sqrt{\frac{I}{mgl}}$

Complex Spring Mass system having Multiple springs in series and Parallel Combination

Series Combination

$K_{eq}=\frac {k_{1}k_{2}}{k_{1}+k_{2}}$

Parallel Combination

$K_{eq}=k_{1}+k_{2}$

Important Questions with Solutions

Question 1

A SHM along an x-axis  Amplitude=.5 m, time to go from one extreme position to other is 2 sec and x=.3m at t=.5 s. Find the general equation of the SHM?

Solution

Let equation  of motion is

$x=A Sin(\omega t + \delta)$

Now A=.5 m  and Time period= 2×2=4 sec

$\omega =\frac {2 \pi }{T} = \frac {\pi}{2} $

Now it is given at =-.5 sec ,x=.3 m

So

$sin  ( \frac {\pi}{4}+ \delta )=\frac{3}{5}$

$\frac {\pi}{4}+ \delta=37^{0}$

$\delta=-8^{0}$

So equation of Motion is

$x=A Sin(\frac{\pi t}{2} -8^{0})$

Question 2

A block of m is connected to a spring of spring constant k and is at rest in the equilibrium position

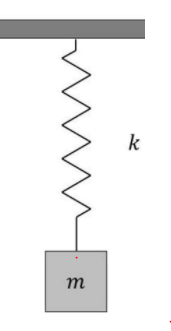
Now the block is displaced by distance c from equilibrium position and imparted a speed v₀ towards down. As a jerk,block execute SHM about its equilibrium position.

Find out

a) Amplitude of the motion

b) equation of the motion

c) Time taken by the block to cross the mean position first time

Solution

Angular frequency is given by

$\omega =\sqrt{\frac{k}{m}}$

we know that velocity at position y is given by

$v=\omega \sqrt{A^2 -y^2}$

Therefore

$v_0=\sqrt{\frac{k}{m}} \sqrt{A^2 -c^2}$

or

$A=\sqrt{\frac{mv_0^2}{k} + c^2}$

Let equation  of motion be

$y=-A Sin(\omega t + \delta)$

at t=0 ,x=-c

$h=A Sin (\delta)$

$\delta= Sin ^{-1} \frac {c}{A}$

So equation of motion is

$y=-A Sin(\omega t + \delta)$

Where  $A=\sqrt{\frac{mv_0^2}{k} + c^2}$  and $\delta= Sin ^{-1} \frac {c}{A}$

Now when the object passes through mean position

$0=-A Sin(\omega t + \delta)$

$\omega t + \delta= \pi$

$t=\frac {\pi – \delta}{\omega }$

Question 3

A particle at the end of a spring executes simple harmonic motion with a period a the corresponding period for another spring is b. Find the period of oscillation(c) of these springs in series ?

Solution

We know that

$Time-period(T) =2 \pi \sqrt{\frac{m}{k}}$

$a =2 \pi \sqrt{\frac{m}{k_1}}$

$b =2 \pi \sqrt{\frac{m}{k_2}}$

$c =2 \pi \sqrt{\frac{m}{k_eq}}$

Now

$\frac{1}{K_eq}=\frac{1}{k_1}  + \frac{1}{k_2}$

So  $c^2 = a^2 + b^2$

Important Material to Read on Simple Harmonic Motion
Complete Study Material at the following link
SHM Study Material
Multiple Problems at the following link
SHM problems and Solution

Must Read Articles to increase grades in Exams

how to study physics problems
Frequently used basic physics equations
Tips on How to write in Examination for better score
How to solve electric force and field problems