Integrating a constant is a fundamental concept in calculus. When you integrate a constant ( c ) with respect to a variable ( x ), the result is a linear function in ( x ). The integration is performed as follows:
$$ \int c \, dx = c \cdot x + C $$
Here, ( C ) represents the constant of integration. This constant is added because when you differentiate a constant, the result is zero, and thus any constant could have been part of the original function before differentiation.
For example, if you integrate the constant 5 with respect to ( x ), you get:
$$ \int 5 \, dx = 5x + C $$
This means that the integral of 5 with respect to ( x ) is a linear function ( 5x ) plus an arbitrary constant ( C ).
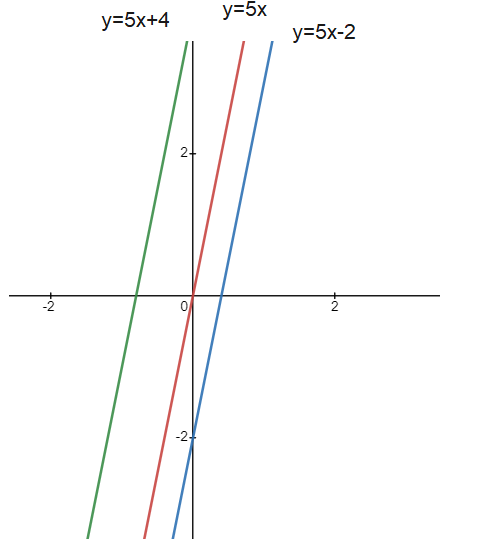
Geometrical Meaning of Integration of constant
Integration of constant 5 represent family of curves as show in below figure .Each of which can be obtained by the shifting any one of the curves parallel to itself
Examples
- Integration of 2:
$$ \int 2 \, dx = 2x + C_1 $$ - Integration of 3:
$$ \int 3 \, dx = 3x + C_2 $$ - Integration of 4:
$$ \int 4 \, dx = 4x + C_3 $$ - Integration of 6:
$$ \int 6 \, dx = 6x + C_4 $$ - Integration of ( \pi ) (Pi is a constant approximately equal to 3.14159):
$$ \int \pi \, dx = \pi x + C_5 $$ - Integration of ( e ) (e is Euler’s number, approximately equal to 2.71828):
$$ \int e \, dx = ex + C_6 $$ - Integration of 0:
$$ \int 0 \, dx = 0x + C_7 = C_7 $$
In each case, the ( C_i ) represents a unique constant of integration for that particular integral. The integral of a constant is a linear function in ( x ), with the slope equal to the constant being integrated.
Definite Integral of constant value
Definite integral will be represent as
$\int _{a}^{b} c \, dx $
To solve this, we use the antiderivative of c, which is cx. So, the integral becomes:
\[
\left[ cx \right]_{a}^{b}
\]
Now, we evaluate this expression at the upper and lower limits of the integral:
\[
= cb -ca
\]
So, the definite integral of \(c \) from \(a\) to \(b \) is \(c(b-a)\).
This result has a geometric interpretation: it represents the area under the curve of (y = c) from (a) to (b), which corresponds to area of the rectangle
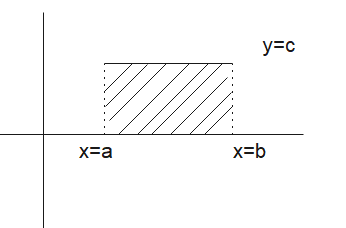
Other Integration Related Articles