Integration of sinx

The integral of the sine function, $ \sin x$, can be found using basic calculus principles. The integral of $\sin x$ with respect to (x) is:

\[
\int \sin x \, dx = -\cos x + C
\]

Here, (C) represents the constant of integration, which is added because the process of integration determines the antiderivative up to an arbitrary constant. This result is derived from the fact that the derivative of $-\cos x$ is $\sin x$.

Integration of sinx by Principal of Derivatives

we can use the fundamental theorem of calculus, which states that if a function f is the derivative of another function F, then the integral of f is F plus a constant.

Now we know that

$\frac {d}{dx} \cos(x) = – \sin(x)$
$\frac {d}{dx} (- \cos(x)) = \sin(x)$
or
$\frac {d}{dx} (- \cos(x) + C) = \sin(x)$

Where C is the constant

Now from fundamental theorem of calculus stated above, we can say that

\[
\int \sin x \, dx = -\cos x + C
\]

Geometrical Meaning of Integration of sinx

Integration of sinx represent family of curves as show in below figure .Each of which can be obtained by the shifting any one of the curves parallel to itself

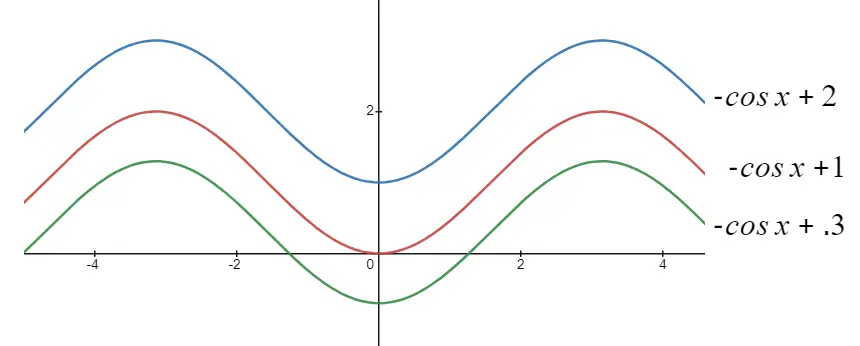
Further if we find the tangents of all these curves at a point x=a on the curve, we have that
$\frac {d}{dx}_0 =sin(a)$

So all the tangents will be parallel at the point x=a

Definite Integration of sinx

Definite integral will be represent as

$\int _{0}^{\pi} \sin x \, dx $

To solve this, we use the antiderivative of (\sin x), which is (-\cos x). So, the integral becomes:

\[
\left[ -\cos x \right]_{0}^{\pi}
\]

Now, we evaluate this expression at the upper and lower limits of the integral:

\[
= -\cos(\pi) – (-\cos(0))
\]

Recall that (\cos(\pi) = -1) and (\cos(0) = 1). Substituting these values in, we get:

\[
= -(-1) – (-1)
\]
\[
= 1 + 1
\]
\[
= 2
\]

So, the definite integral of \(\sin x\) from \(0\) to \(\pi\) is \(2\).

This result has a geometric interpretation: it represents the area under the curve of (y = \sin x) from (0) to (\pi), which corresponds to one complete “hill” of the sine wave from its start to its peak and back to the x-axis.

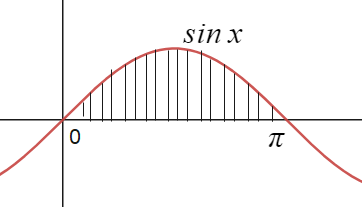
Solved Questions on Integration of sinx

Question 1
Evaluate \(\int_{0}^{2\pi} \sin x \, dx\). What does this value represent in terms of the graph of \(\sin x\)?
Solution
This integral equal zero, as the positive and negative areas under the curve of \(\sin x\) over one full period from \(0\) to \(2\pi)\) cancel each other out.

Question 2
Find the integral \(\int (3\sin x + 2) \, dx\).
Solutions
\(\int (3\sin x + 2) \, dx = -3\cos x + 2x + C\)

Question 3
Evaluate \(\int x \sin x \, dx\).
Solutions
For \(\int x \sin x \, dx\), let \(u = x\) and \(dv = \sin x \, dx\). Then \(du = dx\) and \(v = -\cos x\). Applying integration by parts:
\[ \int x \sin x \, dx = -x \cos x + \int \cos x \, dx = -x \cos x + \sin x + C \]