Magnitude in physics is a measure of the strength or intensity of a physical quantity. It is used to compare various quantities to one another and is frequently expressed as a numerical value. Force, velocity, and energy are a few examples of physical quantities that can be measured by magnitude.
What is magnitude in physics?
In physics, we encounter two kinds of quantities namely scalars and vectors. We also know that scalars only have magnitude and vectors have both magnitude and direction.
In physics, magnitude refers to the size or strength of a quantity, such as a force or a velocity.
To express the magnitude of a physical quantity we need to have its numerical value and unit. A vector quantity is made up of components of a physical quantity in $x$, $y$, and $z$ directions. The magnitude of a vector quantity can be found using a formula that we would discuss in this article.
Magnitude is used to compare and understand the relative sizes and strengths of different physical quantities in physics.
Importance in Physics
It is an important concept in physics because it allows us to compare different physical quantities with each other.
For example, we can compare the magnitude of a force to the magnitude of an acceleration, or we can compare the magnitude of an electric field to the magnitude of a magnetic field.
By measuring and comparing magnitudes, physicists can gain a better understanding of the physical world around them.
Examples of physical quantities with magnitude
Common examples of physical quantities with magnitude include speed, force, energy, electric current, temperature, pressure, and volume.
These physical quantities are usually measured in standard units and are used by physicists to analyze and understand physical phenomena.
A few examples of magnitude in physics are
- Speed: The magnitude of an object’s speed is the distance it travels per unit of time. For example, if a car travels 100 kilometers in 2 hours, its speed has a magnitude of 50 km/h.
- Force: The magnitude of a force is the amount of push or pull that it exerts. For example, a force of 5 newtons is greater in magnitude than a force of 2 newtons.
- Energy: The magnitude of energy is the amount of work that can be done by a force. For example, a 100-watt light bulb has a greater energy magnitude than a 60-watt light bulb.
- Electric current: The magnitude of electric current is the flow of electric charge per unit of time. For example, a current of 1 ampere (A) is greater in magnitude than a current of 0.5 amperes.
- Electric potential difference: The magnitude of electric potential difference is the amount of energy per unit of charge that is transferred between two points in an electric circuit. For example, a potential difference of 6 volts is greater in magnitude than a potential difference of 3 volts.
- Power: The magnitude of power is the rate at which energy is transferred or work is done. For example, a motor that generates 100 watts of power is more powerful than a motor that generates 50 watts of power.
Finding the magnitude of a physical quantity
Scalar and vector quantities both use magnitude as a common factor. We are clear that scalar quantities are those that have only magnitude by definition. Those quantities with both magnitude and direction are considered vector quantities.
To express the magnitude of a physical quantity we need to know two things,
- unit in which the quantity is measured
- The numerical value – expresses how many times the above-mentioned unit is contained in the given physical quantity.
Therefore,
Magnitude og physical quantity = numerical value of physical quantity times size of its unit.
If $n$ is the numerical value of a physical quantity and $u$ is the size of the unit, then, magnitude $Q$ of physical quantity is
$$Q=nu$$
So, when we say that the length of a rod is 5 meters then here in this case
$Q=5\,m$
it means $n=5$ and $u=1\,m$
The size of the unit is different in different systems of units.
For example, Kg (kilogram) and g (grams) are two units to measure the mass of an object. Now, 500gm is equal to .5Kg. Here the actual value of the mass of the object is the same but their magnitude differs according to the conversion rule between grams and Kg (1 Kg = 1000 gm).
The magnitude of a Vector quantity
Sometimes our vector quantity is given in terms of its components. In such case, each component of the vector has a different magnitude along $x$, $y$, and $z$ directions. For example velocity of a moving object is given by a vector
$$\vec v = 2\hat i+6\hat j +9\hat k \,m/s$$
Here in this case,
- $v_x=2m/s$ along $x-axis$
- $v_y=6m/s$ along $y-axis$
- $v_z=9m/s$ along $z-axis$
To understand it further considers the figure given below
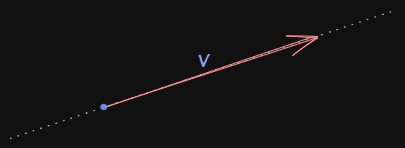
Now if we are looking at a vector as a whole then the length of this vector V represents its magnitude and its direction is along the arrowhead of this vector.
The formula for magnitude depends on the specific physical quantity being measured.
So, in a three-dimensional vector, magnitude is given by the formula:
$|V| = \sqrt{(x^2 + y^2 + z^2)}$
Where $x$, $y$, and $z$ are the vector’s components in the respective directions.
For displacement, velocity, and acceleration vectors, the magnitude is the vector’s length.
For example, in the case of the displacement vector, if the position of a particle is given by the coordinates $(x,y,z)$ then the magnitude of the displacement vector is given by
$|r| = \sqrt{(x^2 + y^2 + z^2)}$
Similarly, for velocity and acceleration vectors, the magnitude is given by
$|v| = \sqrt{(v_x^2 + v_y^2 + v_z^2)}$ and
$|a| = \sqrt{(a_x^2 + a_y^2 + a_z^2)}$
In the case of force, the magnitude can be computed from the net force vector, which is found by adding up all the forces acting on an object.
For example, for a single force $F$ with $x$, $y$, and $z$ components, the magnitude is given by
$|F| = \sqrt{(F_x^2 + F_y^2 + F_z^2)}$
Conclusion
- Magnitude is a scalar quantity, which means it only has a value and no direction. In contrast, vector quantities, such as velocity or force, have both a value (magnitude) and a direction.
- Some physical quantities have defined units of measurement for their magnitudes, such as meters per second for velocity, or newtons for force.
- Magnitude is an important concept in physics, as it allows us to compare and understand the relative sizes and strengths of different physical quantities. It is used in the study of mechanics, thermodynamics, electromagnetism, and many other areas of physics.