In this article find Projectile motion formula for an object fired at an angle and for the object fired horizontally. Find the relevant formula with examples for better understanding.
Projectile motion is a form of motion in which an object or particle (called a projectile) is thrown with some initial velocity near the earth’s surface, and it moves along a curved path under the action of gravity alone.
It is an example of a two-dimensional motion with constant acceleration.
A body moves in a projectile motion when it is thrown at an angle from the horizontal surface or when an object is fired or thrown horizontally from the cliff. This is also observed if an object is thrown at an angle with horizontal from cliff
Projectile Motion of an object fired Horizontally from the top of the tower
Initial Velocity
Horizontal Component
${v_{0x}} = {v_0}$
Vertical Component
${v_{0y}}=0$
Horizontal Acceleration
$a_x=0$
Vertical Acceleration
$a_y=-g$
Equation of Motion
X-coordinate at any point
$x={v_0} t$
Horizontal Component at any point
$v_x={v_0}$
Y-coordinate at any point
$y=H – \frac {1}{2} gt^2 $
Vertical component at any point
$v_y=-gt$
Trajectory Equation
$y=H-\frac {gx^2}{2v_0}$
The trajectory is a parabola
Time of Flight
$t= \sqrt {\frac {2H}{g}}$
Horizontal Range of the Projectile
$R= v_0 \sqrt {\frac {2H}{g}}$
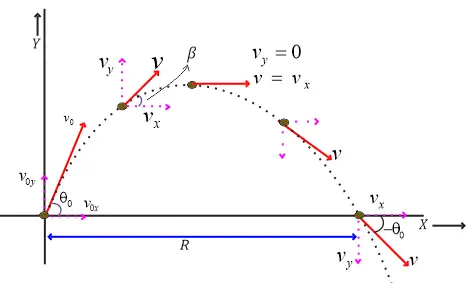
Projectile Motion of an object fired at an angle $\theta _0$ to horizontal
Initial Velocity
Horizontal Component
${v_{0x}} = {v_0}cos{\theta _0}$
Vertical Component
${v_{0y}} = {v_0}sin{\theta _0}$
Horizontal acceleration
$a_x=0$
Vertical Acceleration
$a_y=-g$
Equation of Motion
X-coordinate at any point
$x=(v_0cos{\theta _0})t$
Y-coordinate at any point
$y=(v_0sin{\theta _0})t- \frac {1}{2}gt^2$
Horizontal Component at any point
$v_x=v_0cos{\theta _0}$
Vertical component at any point
$v_y={v_0}sin{\theta _0}-gt$
Trajectory Equation
$y=(tan{\theta _0})x-[\frac {g}{2(v_0cos{\theta _0})^2}]x^2$
This is the equation of the parabola
Time of flight of projectile
$T=\frac {2v_0 sin{\theta _0}}{g}$
Maximum Height reached by Projectile
$H=\frac {v_0^2 sin^2 {\theta _0}}{2g}$
Horizontal Range of the Projectile
$R=\frac {v_0^2 sin {2 {\theta _0}}}{g}$
Special Cases
a. Maximum Range for a given initial velocity is obtained when $ \theta _0=45^0$.
Maximum Range is given as
$R_m=\frac {v_0^2}{g}$
Example : An ball is kicked at the velocity of 18 m/s at an angle 30° from the horizontal. Find the time of flight of the ball,range of the ball. Take $g=10m/s^2$
Solution
Here $v_0=18 m/s$
$\theta _0=30$
$T=\frac {2v_0 sin{\theta _0}}{g}$
$T= \frac {2 \times 18 \times .5}{10} =1.8 sec$
$R=\frac {v_0^2 sin {2 {\theta _0}}}{g}$
$R= \frac {18^2 \times \sqrt {3}}{2 \times 10}=28.05 m$
In Physics it is important to know what is motion? Motion and its study lay the basic foundation for the student who wants to study physics. It is important for students to master these concepts.
If you want to dive further and learn more about motion and kinematics you can consider buying the book
Interactive Physics Part 3.
This book covers most portions of Mechanics. It gives you a thorough grounding in Physics and imparts skills so that you can tackle IIT JEE, Engineering and Medical entrance exams with confidence. The application methods and concepts/misconceptions can be applied to various entrance examinations (IIT JEE, JEE Main, NEET, AIIMS, JIPMER, BITSAT etc.)
For those of you who are interested in video tutorials can look at this video course by udemy
Mastering Kinematics
This course will guide you to solve any, one and two-dimensional kinematics problem, using kinematics equations and solving graphical problems. Through this course, you can learn how to solve relative motion problems such as river crossing problems
DISCLOSURE: THIS POST MAY CONTAIN AFFILIATE LINKS, MEANING I GET A COMMISSION IF YOU DECIDE TO MAKE A PURCHASE THROUGH MY LINKS, AT NO COST TO YOU. PLEASE READ MY DISCLOSURE FOR MORE INFO.