Similar triangles is quite a useful topics for Geometry. It is quite widely used in Physics also. Here are Similar Triangles Formula to help you dela with variety of problems
Formula 1
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio
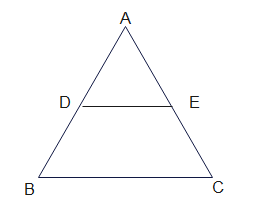
$\frac {AD}{AB} = \frac {AE}{AC}$
Formula 2
If sides are in Proportion, the lines DE || BC
Formula 3
Side and Angles For Similar Triangles
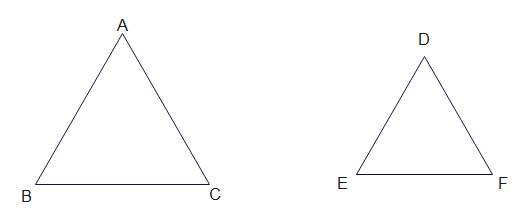
$\Delta ABC \sim \Delta DEF$
$\angle A = \angle D$, $\angle B = \angle E $, $\angle C = \angle F$
$\frac {AB}{DE}=\frac {AC}{DF} =\frac {BC}{EF}$
Formula 4
Perimeter for Similar Triangles
$\frac {AB}{DE}=\frac {AC}{DF} =\frac {BC}{EF} = \frac {\text{perimeter of triangle ABC}}{\text {perimeter of triangle DEF}}$
Formula 5
Area for Similar Triangles
$\frac {\text {Area of triangle ABC}}{\text{Area of triangle DEF}}= \frac {AB^2}{DE^2}=\frac {AC^2}{DF^2} =\frac {BC^2}{EF^2} $
Formula 6
AAA Similarity Criterion
If the three angles are equal to the corresponding angles of other triangles , then the triangles are Similar
If $\angle A = \angle D$, $\angle B = \angle E $, $\angle C = \angle F$
then $\Delta ABC \sim \Delta DEF$ and
$\frac {AB}{DE}=\frac {AC}{DF} =\frac {BC}{EF}$
Formula 7
AA Similarity Criterion
It is same as above . if two angles are same, the third angle will always be same
If $\angle A = \angle D$, $\angle B = \angle E $
then $\angle C= \angle F $ , $\Delta ABC \sim \Delta DEF$ and
$\frac {AB}{DE}=\frac {AC}{DF} =\frac {BC}{EF}$
Formula 8
SSS Similarity Criterion
If the sides of the two triangles are in same proportion, then triangles are similar
$\frac {AB}{DE}=\frac {AC}{DF} =\frac {BC}{EF}$
then $\Delta ABC \sim \Delta DEF$
and $\angle A = \angle D$, $\angle B = \angle E $,$\angle C= \angle F $
Formula 9
SAS Similarity Criterion
if the one angle of a triangle is equal to one angle of other triangles and sides including that angle is proportional, then the triangles are similar
$\frac {AB}{DE}=\frac {AC}{DF} $ and $\angle A = \angle D$
then $\Delta ABC \sim \Delta DEF$
and $\angle B = \angle E $,$\angle C= \angle F $
and $\frac {AB}{DE}=\frac {AC}{DF} =\frac {BC}{EF}$
Formula 10
Pythagoras Theorem
In a right angle triangle
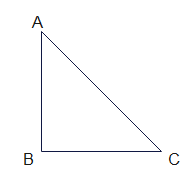
$AC^2 = AB^2 + BC^2$
AC is called the hypotenuse
BC is called the base
AB is the height
Formula 11
RHS Similarity Criterion
If in two right triangles, hypotenuse and one side of one triangle are proportional to the hypotenuse and one side of the other triangle,
then the two triangles are similar
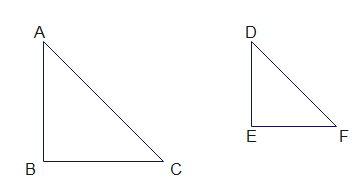
If $\frac {AB}{DE}= \frac {AC}{DF}$ and $\angle B = \angle E= 90^0$
then $\Delta ABC \sim \Delta DEF$
and $\frac {AB}{DE}= \frac {AC}{DF} = \frac {BC}{EF}
and $\angle A = \angle D$ and $\angle C = \angle F$
I hope you will find these formula useful
Related Articles
Similar Triangles Class 10 Notes