This article is only about thermal conductivity formula and its usage in solving various problems. I have discussed thermal conductivity in detail while writing notes in a separate page. Use the link given below to get to know more about it.
The thermal conductivity of a solid is a measure of the ability of the solid to conduct heat through it. The formula for thermal conductivity is
$$K=\frac{Qx}{A\Delta T}$$
Meaning of symbol used in this formula
$K$ – Thermal conductivity
$Q$ – the amount of heat transferred as a result of the temperature difference.
$x$ – the perpendicular distance between two isothermal planes under consideration
$A$ – the area of the cross-section of bar or slab under consideration.
$\Delta T = (T+\Delta T) – T$ – temperature difference between two isothermal planes under consideration.
These terms used in the formula can be seen in the figure given below:-
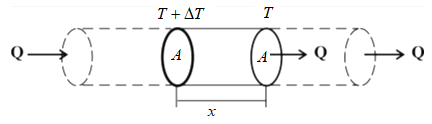
Learn more about isothermal planes on our Heat Conduction page.
Solved examples based on thermal conductivity formula
Question 1 A thermocole cubical icebox of side $30 \, cm$ has a thickness of $5.0 \, cm$. If $4.0\, kg $ of ice is put in the box, estimate the amount of ice remaining after 6 h. The outside temperature is $45^{\circ}C$, and coefficient of thermal conductivity of thermocole is $0.01 J s^{–1} m^{–1} K^{–1}$. [Heat of fusion of water $= 335 \times 103 J kg^{–1}$]
Question-solving strategy:- This is a typical heat transfer question that involves thermal conductivity formula. This is a straight forward question where you are given area $A$, thickness (perpendicular distance between two isothermal surfaces), the time frame for which we have to consider heat transfer and the temperature difference between two isothermal surfaces. We are also given the heat of fusion of water $L$ and from calorimetry relation between $L$ and $Q$ is $Q=mL$. This $Q=mL$ formula would be used for calculating the amount of ice remaining after 6 h.
Solution
Length of each side $= l = 30 cm = 0.3 m$,
Thickness $= x = 5 cm = 0.05 m$
Total surface area of the box, $A = 6\times (side)^2 = 6 \times 0.3 \times 0.3$,
Temperature difference $= T_1 – T_2 = 45 – 0 = 45^{\circ}C$
$0.01 J s^{–1} m^{–1} K^{–1}$
Time $= t = 6 hrs = 6 \times 60 \times 60 \, s$
Latent heat of fusion $= L = 335\times 10^3 \, J/kg$
Total heat entering the box through all six faces ,
$$Q=\frac{KA(T_1 – T_2)t}{x}=\frac{0.01\times 0.54 \times \, 45 \times 6\times 3600}{0.05}=104976 J$$
If $m$ is the mass of ice melted due to this heat then, then
$Q=mL$
or,
$$m=\frac{Q}{L}=\frac{104976\, J}{335\times 10^3 \, J/kg}=0.313\, Kg$$
Mass of ice left after six hours $=4-0.313=3.687\, Kg$
Question 2 Two rods $A$ and $B$ are of equal length . Each rod has its ends at temperatures $T_1$ and $T_2$. What is the condition that will ensure equal rates of flow of heat through the rods $A$ and $B$ ? [IIT]
Question-solving strategy:- This is also a question based on thermal conductivity formula. In question it is asked about a condition that ensures equal rate of flow of heat in both the rods. To find this condition we have to equate rate of flow of heat i.e., $H=\frac{Q}{t}$ for both the rods.
Solution Let $x$ be the length of rods $A$ and $B$. Now the rates of flow of heat through the rods $A$ and $B$ will be equal if,
$$\frac{K_1A_1(T_1 – T_2)}{x}=\frac{K_2A_2(T_1 – T_2)}{x}$$
or,
$$K_1A_1=K_2A_2$$
or,
$$\frac{A_1}{A_2}=\frac{K_2}{K_1}$$
For more information, you can refer the following links (external)