In this post,we will be checking the vertical line test and how is it used. Examples and Problems are also given to help the student. This will also answer the question How do you know if the graph is a function?
What is Vertical line test
A relation (in math) is a function in math if no pair of the relation has the same first elements. On the graph, two points will lie in the same vertical line if and only if the first coordinate of the two points is the same. Therefore if a vertical line intersects the Relation graph at two points then it is not a function. This is called the Vertical line test. If all vertical lines intersect a curve at most once then the curve represents a function.
How to use the it
To use it, take a rule or other straight edge and draw a line parallel to the y-axis for any chosen value of x. If the vertical line you drew intersects the graph more than once for any value of x then the graph is not the graph of a function. If alternatively, a vertical line intersects the graph no more than once, no matter where the vertical line is placed, then the graph is the graph of a function. For example, a curve which is any straight line other than a vertical line will be the graph of a function
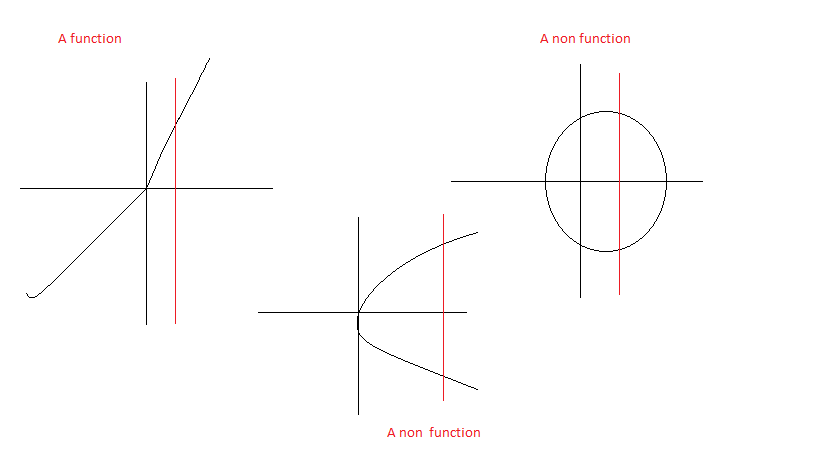
Examples
- Upward Parabola
$y=2x^2$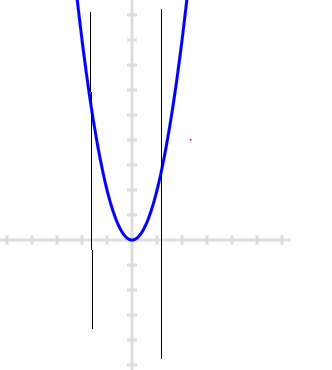
Clearly this is a function 
Clearly this is not a function- The relation
$y=2x^3$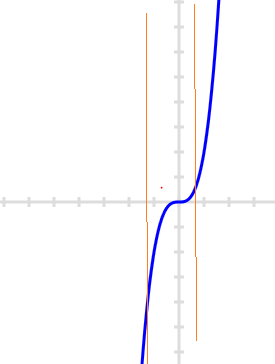
Clearly this is a function - The relation$ \frac {x^2}{a^2} + \frac {y^2}{b^2} =1$
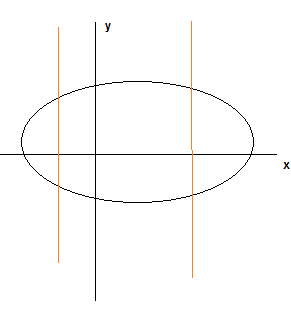
Clearly this is not a function
Practice Problems for Vertical Line test
- Find out if the graph represent functions using Vertical Line check
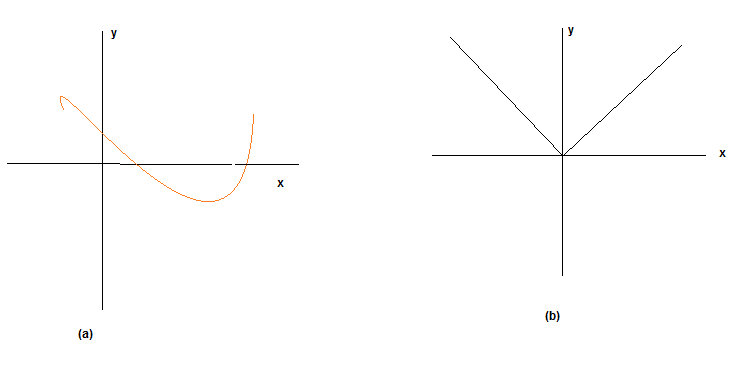
- Find out if the below graph are for function using vertical line test
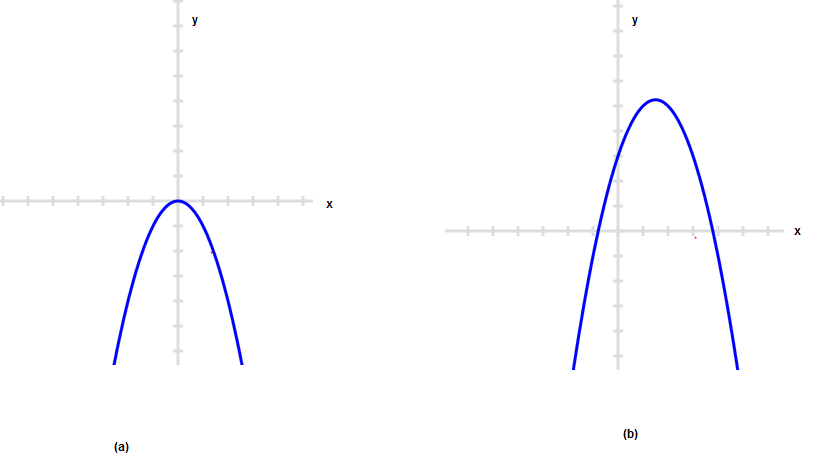
Related Articles
https://en.wikipedia.org/wiki/Vertical_line_test
