What is the dimension of Surface Tension

Dimensional Formula of Surface Tension

In this article, we will find the dimension of Surface Tension
Dimensional formula for Surface tension is

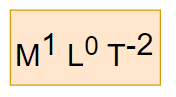
Where
M -> Mass
L-> Length
T -> Time.
We would now derive this dimensional formula.

Derivation for expression of Dimension of Surface Tension

Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of the interface between the plane of the liquid and any other substance.It is denoted by Letter S.Now as per definition
$S = \frac {F}{L}$ –(1)
Where
S-> Surface Tension
F -> Force
L-> Length

Now dimension of Length is given by $[T]$
Lets derive the dimension of Force
Force is defined as product of Mass and acceleration
$F= m \times a$

Dimension of Mass is given by $[M]$
Dimension of Acceleration is derived as
$a= \frac {dv}{dt}$
Where v = velocity, t= time
Lets derive the dimension of Velocity
$v= \frac {dx}{dt}$
or
$v = \frac {d}{t}$
Now
Where
d-> displacement
t -> Time
Now Dimension of Displacement = $[L^1]$
Therefore, dimension of Velocity= $\frac {[L^1]}{[T^1]}=[M^0 L^1T^{-1}]$

So Dimension of Acceleration is given by
$\text{Dimension of Acceleration} =\frac {\text{dimension of velocity}}{\text {dimension of time}}$
$\text{Dimension of Acceleration} =\frac { [M^0 L^1T^{-1}] }{[T]}= [M^0L^1T^{-2}]$
Hence Dimension of Force will be
$ \text{Dimension of Force} = [M^1 ] \times [ M^0L^1T^{-2}] = [M^1L^1T^{-2}]$

Now from equation (1) , we can determine the dimension of Surface Tension as
$ \text{Dimension of Surface Tension} = \frac {\text{Dimension of force}}{ \text{Dimension of Length}} $
$=\frac { [M^1L^1T^{-2}] }{[L]}=[ M^1L^0T^{-2}] $
Unit of Surface Tension is N/m

Try the free Quiz given below to check your knowledge of Dimension Analysis:-

---

Quiz on Dimensional Analysis

---

• <<
• 1
• 2
• 3
• 4
• 5
• >>

1. Which of the following is a dimensionless quantity

Stress

Strain

Specific Heat

Quantity of heat

Question 1 of 5

2. Which of the following pair does not have the same dimensions

work and torque

angular momentum and Planck's Constant

moment of inertia and moment of force

impulse and momentum

Question 2 of 5

3. The dimension of angular velocity is

\([M^0L^0T^{-1}]\)

\([M^2L^0T^{-1}]\)

\([MLT^{-2}]\)

\([ML^2T^{-2}]\)

Question 3 of 5

4. The dimension of torque is

\([ML^{-1}T^{-1}]\)

\([ML^3T^{-3}]\)

\([ML^2T^{-2}]\)

\([MLT^{-2}]\)

Question 4 of 5

5. Which of the following has the dimensions of pressure?

\([M^{-1}L^{-1}]\)

\([MLT^{-2}]\)

\([ML^{-2}T^{-2}]\)

\([ML^{-1}T^{-2}]\)

Question 5 of 5

 Loading...

 

---

Related Articles

1. Dimensional Analysis:- a very good website for physics concepts
2. Work Done Formula
3. Work done by Variable Force
4. dimension of angular momentum
5. Dimension of Force

Note to our visitors:-

Thanks for visiting our website.
DISCLOSURE: THIS PAGE MAY CONTAIN AFFILIATE LINKS, MEANING I GET A COMMISSION IF YOU DECIDE TO MAKE A PURCHASE THROUGH MY LINKS, AT NO COST TO YOU. PLEASE READ MY DISCLOSURE FOR MORE INFO.