Example-1
A object of mass m= 2 kg is subjected by the variable force in x-direction. The force varies as per the below function
$F_x= (3 + .2 x) N$
Find the work done by the force in moving the object from x=0 to x= 5 m?
Solution
$W= \int_{x_a}^{x_b} fdx$
$W= \int_{0}^{5} (3 + .2x) dx = 17.5 J $
Example -2
A particle is acted by the force along x-axis which varies as given in below graph
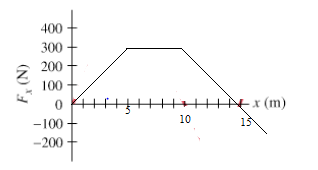
a. Find the work done from x=0 to x=5 m
b. Find the work done from x=5 to x=10 m
c. Find the work done from x=10 to x=15 m
Solution
Work done by will given by the area enclosed
a. work done from x=0 to x=5 m = $ \frac {1}{2} \times 300 \times 5 = 750 N$
b. work done from x=5 to x=10 m = $ 300 \times 5 = 1500 N$
c. work done from x=10 to x=15 m = $ \frac {1}{2} \times 300 \times 5 = 750 N$
Example- 3
A man pushes a trunk on a railway platform which has a rough surface. He applies a force of 100 N over a distance of 10 m. Thereafter, he gets
progressively tired and his applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m.
a. Plot the force applied by the man and the frictional force, which is 50 N versus displacement
b. Calculate the work done by the force applied by Man over 20 m.
c. Calculate the work done by the
frictional forces over 20 m.
d. Calculate the net work done on trunk
Solution
The plot of the force applied by the man (F) and Frictional force (50 N) is given below
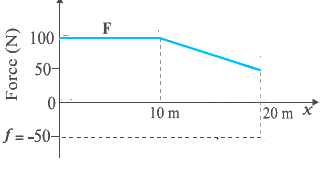
The frictional force is constant and acts in the opposite direction to the applied force.So it is shown as negative in the graph
Now The work done by the man is given by the area enclosed by the Force F in the above graph
Work done= area of the rectangle + area of the trapezium
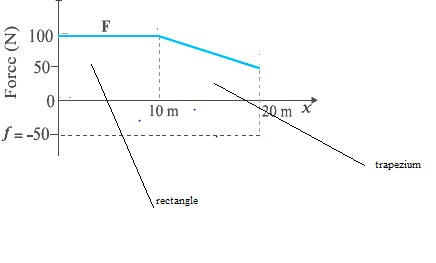
$W= 100 \times 10 + \frac {1}{2} (100 + 50 ) \times 10$
= 1000 + 750
= 1750 J
Now The work done by the frictional force is given by the area enclosed by the friction force (-50 N) in the above graph
Work done= area of the rectangle
$ W = -50 \times 20 = -1000 J $
Net work done= 1750 -1000 = 750 J