In this article, we will look at standard identities as well as some other Algebraic identities. In addition, we will attempt to derive these identities without using the binomial theorem. We’ll also look at some solved examples of problems that use these mathematical identities to solve them.
What is an Algebraic Identity
An Algebraic identity is equality, which is true for all values of the variables in the equality. While an equation is true only for certain values of its variables. An equation is not an identity. These identities are used during the factorization of polynomials.
Why an equation is not an identity?
x+ 2 =5
Now, this is true for x=3 only. So this is not an identity
$(x+1)^2 = x^2 + 2x +1$
Now this is true for x=0,1,2 –. So this is an identity
The Binomial Theorem is used to derive all of the standard Algebraic Identities and is given as:
\begin{array}{l} (a+b)^{n} =\; ^{n}C_{0}.a^{n}.b^{0} +^{n} C_{1} . a^{n-1} . b^{1} + …….. + ^{n}C_{n-1}.a^{1}.b^{n-1} + ^{n}C_{n}.a^{0}.b^{n}\end{array}
Standard Identities
There are four standard Identities
Identity (I)
$(a + b)^2 = a^2 + 2ab + b^2$
Derivation:
$(a + b)^2 = (a + b) (a + b)$
$= a(a + b) + b (a + b)$
$= a^2 + ab + ba + b^2$
$= a^2 + 2ab + b^2$
Identity (II)
$(a – b)^2 = a^2 – 2ab + b^2$
Derivation:
$(a – b)^2 = (a – b) (a – b)$
$= a(a – b) – b (a – b)$
$= a^2 -ab – ba + b^2$
$= a^2 – 2ab + b^2$
Identity(III)
$(a + b) (a – b) = a^2– b^2$
Derivation:
$(a+b)(a – b) = a(a – b) + b (a – b)$
$= a^2 -ab + ba – b^2$
$= a^2 – b^2$
Identity(IV)
$(x + a) (x + b) = x^2 + (a + b) x + ab $
Derivation:
$(x + a) (x + b) = x(x+b) + a (x+b)$
$=x^2 + xb + ax + ab$
$=x^2 + x(a+b) + ab$
Special Cases
(i) for b =a
$(x + a) (x + b) = x^2 + (a + b) x + ab $
$(x+a)^2 = x^2 + 2ax + a^2$
which is the same as identity (I)
(ii) for b =-c,a=-c
$(x + a) (x + b) = x^2 + (a + b) x + ab $
$(x-c)^2 = x^2 – 2cx + c^2$
which is the same as identity (II)
(iii) for b =-a
$(x + a) (x + b) = x^2 + (a + b) x + ab $
$(x+a)(x-a) = x^2 – a^2$
which is the same as identity (III)
(iv)For b=-b
$(x + a) (x – b) = x^2 + (a – b) x – ab$
(v) For a=-a
$(x – a) (x + b) = x^2 + (b – a) x – ab$
(vi) For a=-a and b=-b
$(x – a) (x – b) = x^2 – (a +b) x + ab$
Other Algebraic Identities
Identity (V)
$(x + y + z)^2 = x^2 + y^2 + z^2 + 2xy + 2yz + 2zx$
Derivation:
$(x + y + z)^2 =(x+y+z)(x+y+z)$
$=x(x+y+z) + y ( x+y+z ) + z( x+y+z )$
$=x^2 + xy + xz + yx + y^2 + yz + zx + zy +z^2$
$= x^2 + y^2 + z^2 + 2xy + 2yz + 2zx$
The RHS side is called the expanded form
Identity (VI)
$(x + y)^3 = x^3 + y^3 + 3xy (x + y)$
Derivation:
$(x + y)^3 = (x + y) (x + y)^2$
$= (x + y)(x^2 + 2xy + y^2)$
$= x(x^2 + 2xy + y^2) + y(x^2 + 2xy + y^2)$
$= x^3 + 2x^2y + xy^2 + x^2y + 2xy^2 + y^3$
$= x^3 + 3x^2y + 3xy^2 + y^3$
$= x^3 + y^3 + 3xy(x + y)$
The RHS side is called the expanded form
Identity (VII)
$(x – y)^3 = x^3 – y^3 – 3xy (x – y) $
Derivation:
This can be easily obtained by y=-y in identity (VI)
Identity (VIII)
$x^3 + y^3 + z^3 – 3xyz = (x + y + z)(x^2 + y^2 + z^2 – xy – yz – zx)$
Derivation:
\begin{align*}
(x + y + z)&(x^2 + y^2 + z^2 – xy – yz – zx)\\&=x(x^2 + y^2 + z^2 – xy – yz – zx) + y(x^2 + y^2 + z^2 – xy – yz – zx) \\&+ z(x^2 + y^2 + z^2 – xy – yz – zx)\\
&=x^3 + xy^2 + xz^2 – x^2y – xyz – zx^2 + yx^2+ y^3 + yz^2 – xy^2 – y^2z – xyz \\&+ x^2z + y^2z + z^3 – xyz – yz^2 – xz^2\\
&= x^3 + y^3 + z^3 – 3xyz \end{align*}
Identity (IX)
$(a + b + c)^3 = a^3+ b^3 + c^3 + 3a^2 b + 3a^2c + 3b^2c +3b^2a +3c^2a +3c^2a+6abc$
Derivation:
$ (a + b + c)^3 =(a+b+c)( a + b + c)^2$
Now from identity (V)
\begin{align*}
=&(a+b+c)(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)\\
=&a( a^2 + b^2 + c^2 + 2ab + 2ac + 2bc )+ b( a^2 + b^2 + c^2 + 2ab + 2ac + 2bc ) + \\&c( a^2 + b^2 + c^2 + 2ab + 2ac + 2bc )\\
= &a^3+ b^3 + c^3 + 3a^2 b + 3a^2c + 3b^2c +3b^2a +3c^2a +3c^2a+6abc
\end{align*}
Identity (X)
$x^3 + y^3 = (x + y) (x^2 – xy + z^2 ) $
Derivation:
From identity (VI)
$(x + y)^3 = x^3 + y^3 + 3xy (x + y)$
$x^3 + y^3 = (x+y)^3 – 3xy (x + y)$
$ x^3 + y^3 = (x+y) [(x+y)^2 – 3xy]$
$ x^3 + y^3 = (x+y) (x^2 + y^2 -xy)$
Identity (XI)
$x^3 – y^3 = (x – y) (x^2+ xy + y^2 ) $
Derivation:
From Identity (VII)
$(x – y)^3 = x^3 – y^3 – 3xy (x – y) $
$x^3 – y^3 = (x-y)^3 + 3xy(x-y)$
$x^3 – y^3 = (x-y) [(x-y)^2 +3xy]$
$x^3 -y^3 = (x – y) (x^2+ xy + y^2 ) $
Identity (XII)
If x + y +z =0, then $x^3+ y^3 + z^3= 3 xyz$
Derivation:
From Identity (VIII)
$x^3 + y^3 + z^3 – 3xyz = (x + y + z)(x^2 + y^2 + z^2 – xy – yz – zx)$
Now if x + y +z =0
$ x^3 + y^3 + z^3 – 3xyz = 0$
$ x^3+ y^3 + z^3= 3 xyz$
Identity (XIII)
$x^2 + y^2 + z^2 – xy – yz – zx= \frac {1}{2} [ (x-y)^2 + (y-z)^2 + (x-z)^2]$
Solved Examples
(1) Expand $(3a + 4b + c)^2$
Solution
Comparing the given expression with $(x + y + z)^2$, we find that
x = 3a, y = 4b and z = c.
$(3a + 4b + c)^2 = (3a)^2 + (4b)^2 + (c)^2 + 2(3a)(4b) + 2(4b)(c) + 2(c)(3a)$
$= 9a^2 + 16b^2 + c^2 + 24ab + 8bc + 6a$
(2) Factorise $27x^3 + y^3 + 27z^3 – 27xyz$
Solution
Here, we have
$27x^3 + y^3 + 27z^3 – 27xyz$
$= (3x)3 + y^3 + (3z)^3 – 3(3x)(y)(3z)$
$= (3x + y + 3z)[(3x)^2 + y^2 + (3z)^2 – (3x)(y) – (y)(3z) – (3x)(3z)]$
$= (3x + y + 3z) (9x^2 + y^2 + 9z^2 – 2xy – 3yz – 6xz)$
(3) Expand $(3p + 4q)^3$
Solution
Comparing the given expression with $(x + y)^3$, we find that
x = 3p and y = 4q.
So, using Identity VI, we have:
$(3p + 4q)^3 = (3p)^3 + (4q)^3 + 3(3p)(4q)(3p + 4q)$
$= 27p^3 + 64q^3 + 108p^2q + 144pq^2$
Summary of All the Algebraic Identities
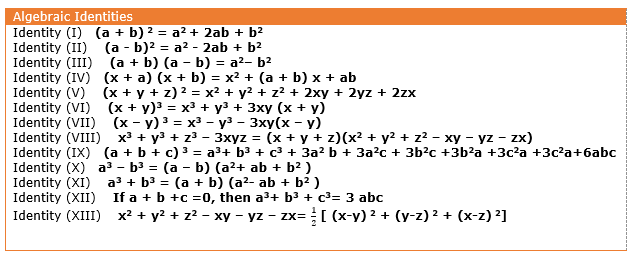
Also Reads
 Skip to content
Skip to content
Very helpful.
Thanks