Algebra Formula for Class 8

Algebra consists of the following topics in Class 8 .
(a) Linear equation
(b) Laws of Exponents
(c) Algebraic Expressions and Identities
(d) Factorization
Here are Algebra Formula for Class 8 topic wise

Linear Equation

What is Linear equation in one Variable

We will restrict the above equation with two conditions

(a) algebraic equation in one variable
(b) variable will have power 1 only

or

An equation of the form ax + b = 0, where a and b are real numbers, such that a is not equal to zero, is called a linear equation in one variables

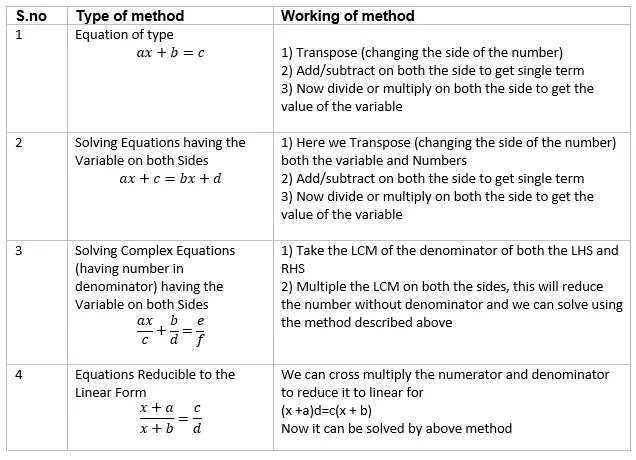
Linear equation in One variable has only one Solution. It can be solved as given below

Laws Of Exponents

Here are the laws of exponents when a and b are non-zero integers and m, n are any integers.

a^-m = 1/a^m

a^m / aⁿ = a^m-n

(a^m )ⁿ     = a^mn

a^m x b^m  = (ab)^m

a^m / b^m   = (a/b)^m

a⁰ =1

(a/b)^-m =(b/a)^m

(1)ⁿ = 1 for infinitely many n. (-1)^p =1  for any even integer p

Algebraic Expressions and Identities

Algebraic expression
It is the expression having constants and variable. It can have multiple variable and multiple power of the variable

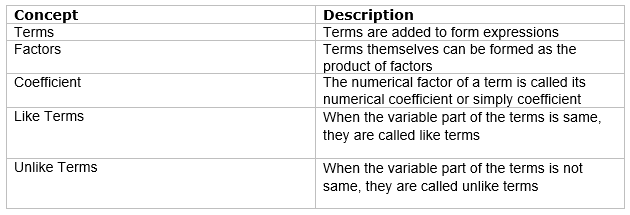
Types

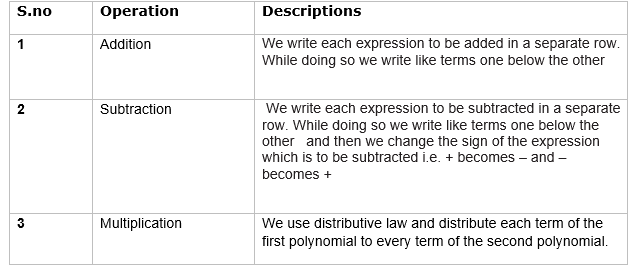
Operation on Algebraic Expressions

Algebraic Identities

(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
 (a + b) (a – b) = a²– b²
(x + a) (x + b) = x² + (a + b) x + ab
(x + a) (x – b) = x² + (a – b) x – ab
(x – a) (x + b) = x² + (b -a) x – ab
(x – a) (x – b) = x² -(a + b) x + ab

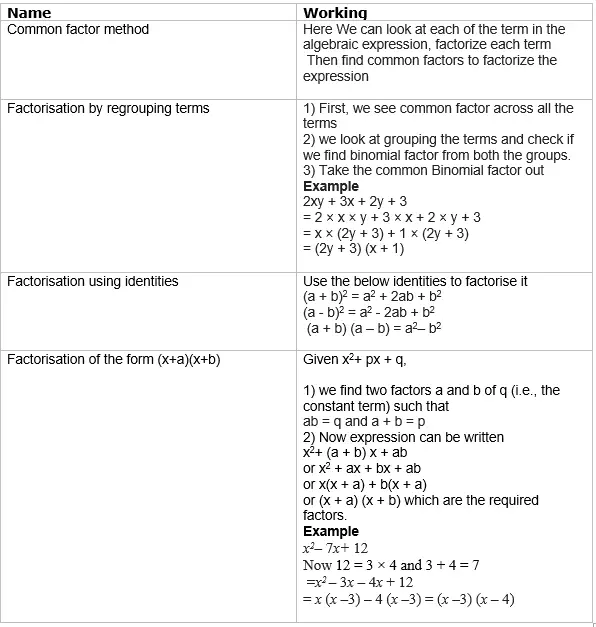
Factorisation

Factorisation of algebraic expression
When we factorise an algebraic expression, we write it as a product of factors. These
factors may be numbers, algebraic variables or algebraic expressions
The expression 6x (x – 2). It can be written as a product of factors.
2,3, x and (x – 2)
$6x (x – 2) =2 \times 3 \times x \times (x – 2)$
The factors 2,3, x and (x +2) are irreducible factors of 6x (x + 2).

Method of Factorisation

Division of algebraic expression

Division of algebraic expression is performed by Factorisation of both the numerator and denominator and then cancelling the common factors.
Steps of Division
(1) Identify the Numerator and denominator
(2) Factorise both the Numerator and denominator by the technique of Factorisation using common factor, regrouping, identities and splitting
(3) Identify the common factor between numerator and denominator
(4) Cancel the common factors and finalize the result

Example
$\frac {48 (x^2yz+ xy^2z+ xyz^2)}{4xyz}$
$=\frac {48xyz (x + y + z)}{4xyz}$
$= 12 (x + y + z)$

Here Dividend=48 (x²yz + xy²z + xyz²)
Divisor=4xyz
Quotient=12 (x + y + z)
So, we have
Dividend = Divisor × Quotient.
In general, however, the relation is
Dividend = Divisor × Quotient + Remainder
When reminder is not zero

Hope you like the post on Algebra Formula for Class 8.

Also Reads

• Learn about the Algebraic Expressions and Identities Notes for Class 8
• BODMAS Rule
• Algebraic Identities