Introduction
A numerical expression can have multiple operations like addition, subtractions, power, Division, multiplication, Brackets.
Example
15 of 6-[18- { 14-(3+2) }]
Now, this is easy to solve like multiple operations on two numbers. We can solve or simplify these types of Numerical expressions using the BODMAS rule.
What is BODMAS Rule
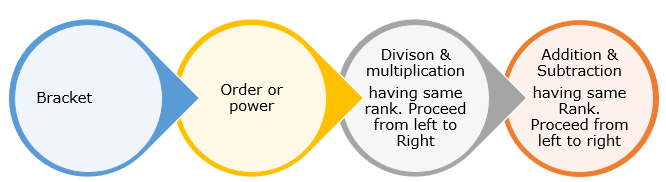
BODMAS is an acronym and it stands for Bracket, Order, Division, Multiplication, Addition, and Subtraction. In Canada, it is called BEDMAS(Bracket, Exponents, Division, Multiplication, Addition and Subtraction In the United States, it is called PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction) These all are synonyms of BODMAS.
-B stands for brackets
-O stands for of, orders, square, roots
-D stands for divisions (÷)
-M stands for multiplication (*)
-A stands for addition (+)
-S stands for subtraction (-)

Now let us how to apply the BODMAS rule to solve the numerical expressions
In order to simplify a numerical expression, we follow the conventions given ahead:
(i) we proceed from left to right.
(ii) The order of working is
brackets -> orders(Exponents or powers) -> division & multiplication -> addition & subtraction.
(iii) The order of brackets is:

Expressions inside the brackets are simplified in order to the letters of the word BODMAS.
(iv) Division and multiplication have the same precedence, so after brackets and orders are over, we just need to move from left to right doing whichever operations come first i.e if multiplication comes first, then do multiplication
(v)Similarly Addition and subtraction have the same precedence, so after brackets,orders, division and Multiplication are over we just need to move from left to right doing whichever operation comes
BODMAS Rule Examples
Lets us see now few Examples
(1) 15 of 6-[18- { 14-(3+2) }]
Applying First the bracket rule
=15 of 6-[18- { 14-5 }]
Applying Again the bracket rule
=15 of 6-[18- 9]
Applying Again the bracket rule
=15 of 6-9
Now Multiplication comes before Subtraction
=90 -9 = 81
(2) $2 \times 5 + 50 \div 2$
Here Multiplication and division have same ran, so we just need to move from left to right doing whichever operations comes first
$=10 + 25$
$=35$
(3) $50 \times 5 \div 10$
Here Multiplication and division have the same ran, so we just need to move from left to right doing whichever operations come first
$=250 \div 10$
=25
(4) $25 \div 5 \times 5$
Here Multiplication and division have the same ran, so we just need to move from left to right doing whichever operations come first
$=5 \times 5$
$=25$
BODMAS Exercise
(5) 105+[19-{2 of 6+(3-2)}]
Answer
= 105 + [19 -{2 of 6 + 1}]
=105 + [19 – {12 + 1}]
=105 + [19 -13]
=105 + 6=111
(6) $\frac{5}{9} \div (1\frac{1}{3}+\frac{4}{9})+\frac{3}{8}$
Answer
$=\frac{5}{9} \div (\frac{4}{3}+\frac{4}{9})+\frac{3}{8}$
Applying the bracket rule
$=\frac{5}{9} \div \frac {16}{9} + \frac{3}{8}$
$=\frac {5}{9} \times \frac {9}{16} + \frac{3}{8}$
$=\frac {5}{16} + \frac{3}{8}$
$=\frac {11}{16}$
(7) $\frac{2}{7} – \frac {1}{6} \ of \ \frac {6}{7} \div \frac {4}{7} – 1\frac {1}{3} + 5$
Answer
$=\frac{2}{7} – \frac {1}{7} \div \frac {4}{7} – 1\frac {1}{3} + 5$
$=\frac{2}{7} – \frac {1}{4} – \frac {4}{3} + 5$
$=\frac {24 – 21 – 112 + 420}{84}= \frac {311}{84}$
(8) $(105 + 206) – 550 \div 5^2 + 1$
Answer
$= 311 – 550 \div 5^2 + 1$
$= 311 – 550 \div 25 + 1$
$=311 – 22 + 1$
=290
(9) 1.5{3.9-(4.5-3.2 × 0.5)}
Answer
= 1.5 { 3.9 – (4.5 – 1.6)}
=1.5 {3.9 – 2.9}
=1.5
(10) 39-[23-{29- (17-9-3)}]
Answer
=39 – [23 -{29 -5}]
=39 – [23 – 24]=39 + 1= 40
(11) $\frac{2}{3} of (\frac{1}{4}+ \frac {1}{2} + \frac {3}{8}) \div \frac {3}{2}$
Answer
$=\frac{2}{3} of (\frac {2+ 4 +3}{8}) \div \frac {3}{2}$
$=\frac{2}{3} of (\frac {9}{8}) \div \frac {3}{2}$
$=\frac{2}{3} of \frac {9}{8} \div \frac {3}{2}$
$= \frac {3}{4} \div \frac {3}{2}$
$= \frac {1}{2}$
(12) $\frac {2}{3} – \frac {1}{2} – \frac {1}{3} \ of \frac {1}{2}$
Answer
$=\frac {2}{3} – \frac {1}{2} -\frac {1}{6}$
=0
(13) $5+ 5 \ of \ 5 \div 5 \ of \ 5 \times 5$
Answer
$=5+(5 \ of\ 5) \div 5 \ of \ 5 \times 5$
$=5 + 25 \div 5 \ of \ 5 \times 5$
$=5+ 5 \ of\ 5 \times 5$
$=5+ (5 \ of \ 5) \times 5$
$=5+ 25 \times 5$
$=5+125$
$=130$
(14) $\frac {5}{6} – \frac {2}{3} \ of \ \frac {1}{3} + \frac {1}{9}$
Answer
$=\frac {5}{6} – \frac {2}{9} + \frac {1}{9}$
$=\frac {13}{18}$
Further Reference
https://en.wikipedia.org/wiki/Order_of_operations
Algebraic Identities
Algebra Formula for Class 8
 Skip to content
Skip to content