This article,i am explaining Inequalities Rules and how to solve inequalities
What is inequalities
In mathematics, an inequality is a relation that holds between two values when they are different
Solving linear inequalities is very similar to solving linear equations, except for one small but important detail: you flip the inequality sign whenever you multiply or divide the inequality by a negative
Symbols used in inequalities or Inequalities Signs
The symbol < means less than. The symbol > means greater than.
The symbol < with a bar underneath means less than or equal to. Usually, this is written as $\leq$
The symbol > with a bar underneath means greater than or equal to. Usually, this is written as $\geq $
The symbol $\ne $ means the quantities on the left and right sides are not equal
Examples
a < b means a is less than b or b is greater a
a $\leq$ b means a is less than or equal to b
a > b means a is greater than b
a $\geq $ b means a is greater or equal to b
Inequalities Rules
It can be divided into part
a. Things which can be done in inequality and it does change the sign
b. Things which change the sign of the inequality
Things are which are safe to do in inequality which does not change in direction
1. addition of same number on both sides
$a > b$
$a+c > b +c$
2. Subtraction of same number on both sides
$a > b$
$a-c > b-c$
3. Multiplication/Division by same positive number on both sides
$a > b$
if c is positive number then
$ac > bc$
or
$ \frac {a}{c} > \frac {b}{c}$
Things which changes the direction of the inequality
1. swapping the left and right sides
$a > b$
$b < a$
2. Multiplication/Division by negative number on both sides
$a > b $
$ -a < -b $
3. Don’t multiple by a variable whose values you don’t know as you don’t know the nature of the variable
Another Important Concept which we must keep in mind while work on inequalities is a Number line
Concept Of Number line
A number line is a horizontal line that has points that correspond to numbers. The points are spaced according to the value of the number they correspond to; in a number line containing only whole numbers or integers, the points are equally spaced.
It is very useful in solving problems related to inequalities and also representing it
Suppose x >2(1/ 3), this can represent this on a number line like that
How to solve inequalities questions in one variable
We will check out how to solve inequalities for both Linear, Quadratic and Rational Fraction
(1)Simplify the Linear inequality
$x- 2 > 2x+15$
$-15 -2 > 2x -x $
$ -17 > x$
$ x < -17$
(2) Simplify the quadratic inequalities
x2-5x+6 > 0
Which can be simplified as
(x-2)(x-3) > 0
or this can be done using the equal sign in inequalities and solve it to find endpoints i,e 2, and 3 in the above case.
Now plot those points on the Number line clearly
Now start from the left of most left point on the Number line and look out the if inequalities look good or not. Check for greater,less than, and inequalities at all the endpoints
So in the above case of
x2-5x+6 > 0
We have two ends points 2,3
Case 1
So for x < 2 ,Let take x=1,then (1-2)(1-3) > 0
2 > 0
So it is good
So This inequalities is good for x < 2
Case 2
Now for x =2,it makes it zero,so not true. Now takes the case of x > 2 but less 3.Lets takes 2.5
(2.5-2)(2.5-3) > 0
-.25 > 0
This is not true so this solution is not good
Case 3
Now lets take the right most part i.e x > 3
Lets take x=4
(4-2)(4-3) > 0
2> 0
So it is good.
Now the solution can either be represented on a number line or we can say like this
$(-\infty,2)\cup (3,\infty)$
(3) Simplify the rational or fractional inequality
$ \frac {(x – 3)}{(x + 5)} > 0$
Solution
Method A
(1) Let’s find the endpoints of the equation
Here it is clearly
x=3 and x=-5
(2) Now plots them on the Number line
(3) Now let’s start from the left part of the most left number
i.e
case 1
x < -5 ,Let takes x=-6 (-6-3)/(-6+5) > 0
3 > 0
So it is good
Case 2
Now take x=-5
as x+5 becomes zero and we cannot have zero in denominator,it is not the solution
Case 3
Now x > -5 and x < 3, lets take x=1 (1-3)/(1+5) > 0
-1/6 > 0
Which is not true
Case 4
Now take x =3,then
0> 0 ,So this is also not true
case 5
x> 3 ,Lets x=4
(4-3)(4+5) > 0
1/9 > 0
So this is good
So the solution is
x < -5 or x > 3
or
$(-\infty,-5)\cup (3,\infty)$
Method B
(1) the numerator and denominator must have the same sign. Therefore, either
x – 3 > 0 and x + 5 > 0,
or
(2) x – 3 < 0 and x + 5 < 0.
Now, (1) implies x > 3 and x > -5.
Which numbers are these that are both greater than 3 and greater than -5?
Clearly, any number greater than 3 will also be greater than -5. Therefore, 1) has the solution
x > 3.
Next, (2) implies
x < 3 and x < -5.
Which numbers are these that are both less than 3 and less than -5?
Clearly, any number less than -5 will also be less than 3. Therefore, (2) has the solution
x < -5.
The solution, therefore, is
x < -5 or x > 3
Some Important points to note
1) We cannot have zero in denominator
2) We should be checking for inequalities at all the end points
Some Problems to practice
1. $2x > 9$
2. $x + 5 > 111$
3. $3x < 4$
4. $2(x + 3) < x+ 1$
5. $x^2 -1 < 0$
6. $\frac {x-1}{x+5} < 0$
7. $x^2 -5x + 6 > 0$
8. $\frac {x-5}{x+1} < 0$
Related Articles
IIT jee questions on relations and functions
Vedic maths tricks
how to study maths
how to solve assertion reason questions
sin cos tan table
https://en.wikipedia.org/wiki/Inequality_(mathematics)
 Skip to content
Skip to content
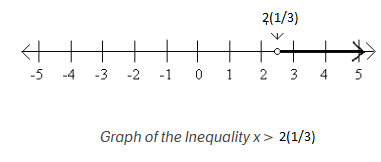
Please send it again to me