How to solve Kinematics problems

Here are some good points on How to solve Kinematics problems

Motion in a One Dimension

We have given a detailed description on below Link
how to solve motion in one dimension problem

Motion in a Two dimensional Plane

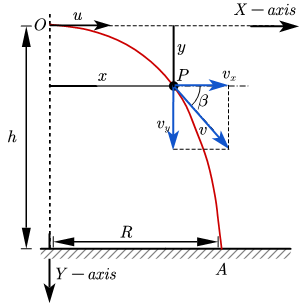
• Select a coordinate system and resolve the initial velocity vector into x and y
  components.
• Find out acceleration in each direction and solve in each direction according to one rectilinear motion equation.
• if the acceleration is in vertical direction only.Follow the techniques for solving constant-velocity problems to analyze the horizontal motion. Follow the techniques for solving constant-acceleration problems to analyze the vertical motion. The x and y motions share the same time of flight t.
• There might be question about trajortory in the Problem ,find out the motion in x and y direction with respect to time from previous point.And then find the value of t from one equation and then put that value in another equation to find out the equation of trajactory

Motion in a Three dimensional Plane

• Select a coordinate system and resolve the initial velocity vector into x , y and z components
• Find out acceleration in each direction and solve in each direction according to one rectilinear motion equation.

Uniform Circular Motion

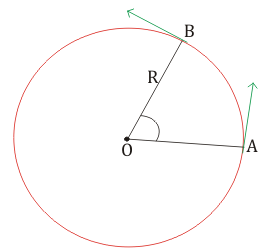
• Draw a simple, neat diagram of the system.
• Firstly consider the origin of the forces acting on the each object.To do this find out the field forces acting on the each object.Wherever contact in available account the contact force carefully
• Find out the force acting on the body.The resultant force should provide the required centripetal required for Circular motion
• Centripetal force$F_{C}=\frac{mv^2}{R}$ will give the velocity accordingly.

Hope this post helps in How to solve Kinematics problems. Please do provide the feedback

Helpful Articles

Acceleration formula
Circular Motion Physics
Laws of motion practice paper for class 11 physics
how to study physics problems
Solving physics problems
Describing Motion and Rest