Complex Numbers Formulas Sheet – Complete Guide PDF

Complex Numbers

Complex numbers are the numbers of the form $a+ ib$ where $i= \sqrt {-1}$  and a and b are real numbers

Algebra for i

$i= \sqrt {-1}$
$i^2= -1$
$i^3 =i \times i^2= -i$
$i^4= i^2 \times i^2 = 1$
$i^{4n} =1$
$i^n + i^{n+1} + i^{n+2} + i^{n+3} =i^n( 1 + i +i^2 + i^3 ) = i^b(1 + i -1 -i)=0$

Addition of Complex Numbers

Let z₁ = x₁ + iy_{1  ­} and z₂ = x₂ + iy₂  z₁ +z₂ = (x₁ + x₂) + i(y₁ + y₂)

Subtraction of Complex Numbers

Let z₁ = x₁ + iy_{1  ­} and z₂ = x₂ + iy₂  z₁ -z₂ = (x₁ – x₂) + i(y₁ – y₂)

Multiplication of Complex numbers

Let z₁ = x₁ + iy_{1  ­} and z₂ = x₂ + iy₂ 

z₁ z₂ = (x₁ + iy₁ ) (x₂ + iy₂  ) =(x₁x₂ – y₁y₂) +i(x₁y₂ +x₂y₁)

Multiplicative Inverse

Let z= a+ ib , Then Multiplicative inverse is given as
$\frac {1}{z}=z^{-1} = \frac {1}{a+ ib} = \frac {a}{a^2 + b^2} – \frac {ib}{a^2 + b^2}$

Division of Complex Numbers

Let z₁ = x₁ + iy_{1  ­} and z₂ = x₂ + iy₂ 
z₁ /z₂ = (x₁ + iy₁ ) /(x₂ + iy₂  ) =z₁ z₂^-1

Conjugate of Complex Number

If z= x+iy then Conjugate is given by $\bar{z} = x-iy$

Properties of Conjugate of Complex Number

If z= x + iy

• $\bar {\left( \bar{z} \right)}= z$
• $ z + \bar{z} = 2 Re(z) = 2x$
• $ z – \bar{z} = 2 Im(z) = 2iy$
• If $ z + \bar{z} = =0$, then $z=-\bar{z} $ and z is purely Imaginary
• $\overline {z_1 + z_2} = \bar{z_1} + \bar{z_2}$
• $\overline {z_1 – z_2} = \bar{z_1} – \bar{z_2}$
• $\overline {z_1 z_2} = \bar{z_1} \bar{z_2}$
• $\overline {z^n} = \left( \bar{z} \right)^n$

Modulus of complex Number

If z= z + iy, then modulus is defined

$|z| = \sqrt {x^2 + y^2}$

Properties of Modulus of complex Number

• $|z| \geq 0$
• If |z| = 0 , then z=0
• |z| > 0, then $z \ne 0$
• $ -|z| \leq Re(z) \leq |z|$
• $ -|z| \leq Img(z) \leq |z|$
• $z \bar{z} =|z|^2$
• $|z|=|-z|$
• $|z_1 z_2| = |z_1||z_2|$
• $|\frac {z_1}{z_2}| = \frac {|z_1|}{|z_2|}$
• $|z_1 + z_2| \leq |z_1| + |z_2|$
• $|z_1 + z_2| \geq ||z_1| – |z_2||$
• $ ||z_1| – |z_2|| \leq |z_1 + z_2| \leq |z_1| + |z_2|$
• $|z_1 – z_2| \leq |z_1| – |z_2|$
• $|z^n| = |z|^n$
• $|z_1 + z_2|^2 = |z_1|^2 + |z_2|^2 + (z_1 \bar{z_2} + z_2 \bar{z_1})$
• $|z_1 – z_2|^2 = |z_1|^2 + |z_2|^2 – (z_1 \bar{z_2} + z_2 \bar{z_1})$
• $|z_1 + z_2|^2 + |z_1 – z_2|^2 =2 |z_1|^2 +2 |z_2|^2$
• $|az_1 +b z_2|^2 + |bz_1 -a z_2|^2 =(a^2 + b^2)( |z_1|^2 + |z_2|^2)$

Argand Diagram

Complex number $z=a +ib$ can be represented by a point P (a, b) on a x-y plane. The x -axis represent the real part while the y-axis represent the imaginary part

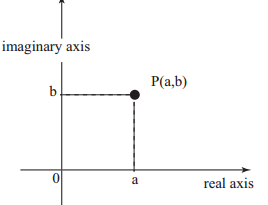
Important points
(1) The length OP is called the module of z and is denoted by $|z| =\sqrt {x^2 + y^2}$
(2) Purely real number lies on X-axis while purely imaginary number lies on y-axis
(3) The Line OP makes an angle $\theta$ with the positive direction of x-axis in anti-clockwise sense is called the argument or amplitude of z
It is given by
$arg (z) = \tan^{-1} \frac {y}{x}$
The unique value of $\theta$ such that $-\pi < \theta \leq \pi$  is called the principal value of the amplitude or principal argument
(4) The principal argument of the complex number is find using the below steps
Step 1) for z=a+ib , find the acute angle value of $\theta =tan^{-1} \frac {|y|}{|x|}$
Step 2) Look for the values of a ,b
if (a, b) lies in First quadrant then Argument=$\theta$
if (a, b) lies in second quadrant then Argument =$\pi -\theta$
if (a, b) lies in third quadrant then Argument =$-\pi + \theta$
if (a, b) lies in Fourth quadrant then Argument =$-\theta$

Properties of Argument of Complex Numbers

• $arg (z_1z_2)= arg(z_1) + arg (z_2) + 2k \pi$
• $arg (\frac {z_1}{z_2})= arg(z_1) – arg (z_2) + 2k \pi$
• $arg (\frac {z}{\bar{z}})= 2 arg(z) + 2k \pi$
• $arg (\bar{z})= – arg(z) $
• $arg (z^n)= n arg(z) + 2k\pi $

Where k is a integer such that Arg lies between $-\pi$ and $\pi$

Polar Representation

$z= |z| (cos (arg) + i sin(arg)$

Here arg is the principal argument of the complex number

we can write this as

$z= r(cos \theta + \sin \theta)$
where r =|z| and $\theta$ is the principle argument

Euler form

For any real number x, e^ix = cos x + i sin x
Let z be a non zero complex number; we can write z in the polar form as,
$z = r(cos \theta + i sin \theta ) = re^{i \theta}$, where r is the modulus and $\theta$ is argument of z.

Important point

(1) Multiplying a complex number z with $e^{i \alpha}$ gives

$z \times e^{i \alpha} = r e^{i \theta} \times e^{i \alpha} = r e^{i(\alpha + \theta)}$

(2) $e^{i \theta} + e^{-i \theta} = 2 \cos \theta$

(3) $e^{i \theta} – e^{-i \theta} = 2 i\sin \theta$

(4) $e^{i \theta} + e^{-i \alpha} = e^{i (\theta + \alpha)/2} 2 \cos (\theta – \alpha)/2$

(5) $e^{i \theta} + 1 = e^{i \theta /2} 2 \cos \theta /2$

(6) $e^{i \theta} – e^{-i \alpha} = e^{i (\theta – \alpha)/2} 2 i\sin (\theta – \alpha)/2$

(7)$e^{i \theta} – 1 = e^{i \theta /2} i 2 \sin \theta /2$

Logarithm of the Complex Number

$log _{e} z = log _ {e} |z| e^{i\theta} = log_{e} |z| + i \theta$

General Form

$log _{e} z = log_{e} z + 2n \pi i $

De Moivre’s theorem

De Moivre’s theorem states following cases

• Case I It states that for any integer n,
  
  $(cos \theta + i sin \theta)^n = cos (n \theta) + i sin (n\theta)$
  
• Case II if n is of the form p/q where p, q are integers and q > 0
  then
  $(cos \theta + i sin \theta)^n =cos (2k \pi+ \theta)p/q + sin (2k \pi+ \theta)p/q$
  Where k=0,1,2,…q-1

Important points

$(cos \theta _1 + i sin \theta_1) (cos \theta _2 + i sin \theta_2) (cos \theta _3 + i sin \theta_3) =cos (\theta _1 + \theta _2 + \theta _3) + i sin (\theta _1 + \theta _2 + \theta _3)$

$(cos \theta – i sin \theta)^n = \cos n \theta – i \sin n\theta$

$(sin \theta + i cos \theta)^n = (-1)^n (\cos n \theta – i \sin n\theta )$

$(sin \theta – i cos \theta)^n = (-1)^n (\cos n \theta + i \sin n\theta)$

$\frac {1}{cos \theta + i sin \theta} = cos \theta – i sin \theta $

How to find the roots of the equation

$(a+ ib)^{p/q}$ where p and q are integers and $q \ne 0$

$(a + ib) = r (\cos \theta + i \sin \theta)$
then $(a+ ib)^{p/q} = r^{p/q} ( \cos \theta + i \sin \theta)^{p/q}$

$=r^{p/q}(\cos \frac {(2k \pi+ \theta)p}{q} + \sin \frac {(2k \pi+ \theta)p}{q} )$

Where k=0,1,2,…q-1

Cube Root of Unity

$z^3 -1=0$
$(z-1)(z^2 + z +1)=0$
$z = 1, \frac {-1 \pm i \sqrt 3}{2}$

We define them as

$\omega = \frac {-1 + i \sqrt 3}{2}$
$\omega ^2 = \frac {-1 – i \sqrt 3}{2}$

Important points

• $1 + \omega + \omega ^2 =0$
• $\omega ^3 =1$
• $\omega ^4 = \omega$
• $\omega ^{3n +1} = \omega$
• $\omega ^{3n +2} = \omega ^2$
• $a^2 + ab + b^2 = (a- b \omega)(a – b\omega ^2)$
• $a^2 – ab + b^2 = (a+ b \omega)(a + b\omega ^2)$
• $a^3 + b^3= (a+b) (a + b \omega) (a + b \omega ^2)$
• $a^3 – b^3= (a-b) (a – b \omega) (a – b \omega ^2)$

nth root of Unity

$z^n -1 =0$
$z^n =1$
$z = 1^{1/n} = (cos 2 k \pi + i \sin 2k \pi)^{1/n}$
$= cos \frac {2 k \pi}{n} + i sin \frac {2 k \pi}{n}$

where k=0,1,2,…n-1

If $\alpha = cos \frac {2 \pi}{n} + i sin \frac {2 \pi}{n}$

(A) Sum of the nth Roots of Unity

$1 + \alpha + \alpha ^2 + \alpha ^3 + ..+ \alpha ^{n-1} = \frac {1 (1 – \alpha ^n)}{1 – \alpha}$
Now as $\alpha ^n =1$, Hence
$1 + \alpha + \alpha ^2 + \alpha ^3 + ..+ \alpha ^{n-1} =0$
So sum of the roots are the nth root of unit is zero

(B) Product of the nth Roots of Unity

$1 \times \alpha \times \alpha ^2 \times \alpha ^3 \times ..\times \alpha ^{n-1} = \alpha^{ 1 + 2 +…(n-1)}=\alpha ^{n(n-1)/2}$
$= (-1)^{n-1}$

Cube root of Any Number

$x^3=a$ is given as

$a^{1/3} , a^{1/3} \omega , a^{1/3} \omega ^2$