What is converse of Pythagoras theorem?
In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right
angle
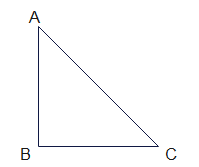
If $AC^2 = AB^2 + BC^2$
then $\angle ABC =90^0$
Proof of converse of Pythagoras theorem
Let ABC be the triangle and given
$AC^2 = AB^2 + BC^2$
To Prove: $\angle ABC =90^0$
Proof:
Lets us construct a triangle PQR right angled at Q such that PQ = AB and QR = BC
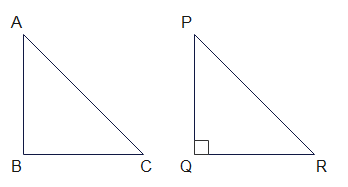
Now in right angle triangle PQR , By Pythagoras theorem
$PR^2 = PQ^2 + QR^2$
or
$PR^2 = AB^2 + BC^2$ ( as PQ = AB and QR = BC)
Therefore
$PR^2 = AC^2$
PR=AC
In triangle ABC and PQR
PQ = AB , QR = BC, PR=AC
By SSS congruence
$\Delta ABC \cong \Delta PQR$
Now from CPCT
$\angle B = \angle Q = 90$
Hence Proved
Examples
Question 1: Given a triangle with sides of length 6 cm, 8 cm, and 10 cm, is the triangle right-angled?
Answer:
Check if 10² = 6² + 8².
100 = 36 + 64
100 = 100
Yes, the triangle is right-angled.
Question 2: A triangle has sides measuring 7 cm, 24 cm, and 25 cm. Determine whether the triangle is right-angled or not.
Answer:
Check if 25² = 7² + 24².
625 = 49 + 576
625 = 625
Yes, the triangle is right-angled.
Question 3: Can a triangle with side lengths of 5 cm, 12 cm, and 14 cm be a right-angled triangle? Use the converse of Pythagoras Theorem to justify your answer.
Answer:
Check if 14² = 5² + 12².
196 = 25 + 144
196 = 169
No, the triangle is not right-angled.
Question 4:
Determine if a triangle with side lengths of 9 cm, 40 cm, and 41 cm is a right-angled triangle.
Answer:
Check if 41² = 9² + 40².
1681 = 81 + 1600
1681 = 1681
Yes, the triangle is right-angled.
Question 5: A triangle has sides of length 15 cm, 20 cm, and 25 cm. Use the converse of Pythagoras Theorem to check if the triangle is right-angled.
Answer: Check if 25² = 15² + 20².
625 = 225 + 400
625 = 625
Yes, the triangle is right-angled.
Related Articles
Pythagorean Triples Formula
Pythagoras Theorem
Similar Triangles Notes