Pythagoras Theorem : Proof, Formula and examples

Introduction to Pythagoras Theorem

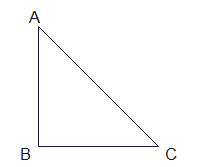
• Pythagoras Theorem is a fundamental concept in mathematics that establishes a relationship between the sides of a right-angled triangle. It is named after the ancient Greek mathematician Pythagoras
• This theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides

$AC^2 = AB^2 + BC^2$

Pythagoras Theorem Formula

The Pythagoras Theorem can be expressed using the following formula:

c² = a² + b²

Where:

• c represents the length of the hypotenuse
• a and b represent the lengths of the other two sides

Pythagoras Theorem Proof using Similar Triangles

Let ABC be a right angle triangle with B=90, let BD is perpendicular to AC

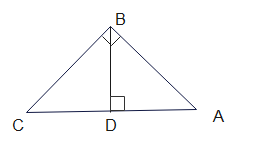
In triangle ABC and BDC

$\angle ABC = \angle BDC$
$\angle BCA = \angle BCD$
From AA Similarity criterion
$\Delta ABC \sim BDC$

Hence

$\frac {AC}{BC}= \frac {BC}{DC}$
or $BC^2 = AC . DC$ -(1)

In triangle ABC and BDA

$\angle ABC = \angle BDA$
$\angle BAC = \angle BAD$
From AA Similarity criterion
$\Delta ABC \sim ADB$

Hence

$\frac {AB}{AD}= \frac {AC}{AB}$
or $AB^2 = AD . AC$ -(2)

Adding equation (1) and (2)

$AB^2 + BC^2 = AC( AD + DC)= AC^2$

Hence proved

Pythagoras Theorem Proof using paper and pencil

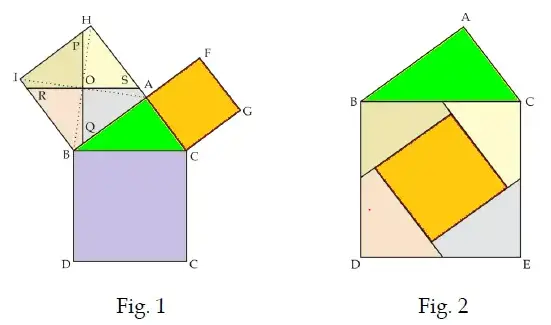
1. Take a card board of size say 20 cm x 20 cm.
2. Cut any right angled triangle and paste it on the cardboard. Suppose that its sides are a, b and c.
3. Cut a square of side a cm and place it along the side of length a cm of the right angled triangle.
4. Similarly cut squares of sides b cm and c cm and place them along the respective sides of the right angles triangle.
5. Color the diagram as shown in below figure. You can choose any other color if you want
6. Join BH and AI. These are two diagonals of the square ABIH. The two diagonals intersect each other at the point O.
7. Through O, draw RS||BC.
8. Draw PQ, the perpendicular bisector of RS, passing through O.
9. Now the square ABIH is divided in four quadrilaterals. Colour them as shown in figure.
10. From the square ABIH cut the four quadrilaterals.
11. Now arrange them as given above and You will see the sum of square of a and b matches square of c in second figure

Examples and Solutions

Question 1: In a right-angled triangle, the lengths of two sides are 3 cm and 4 cm. Determine the length of the hypotenuse.

Solution: Using Pythagoras Theorem (c² = a² + b²), we can find the length of the hypotenuse.

Given:

• a = 3 cm
• b = 4 cm

Now, substitute the values into the formula:

c² = 3² + 4²
c² = 9 + 16
c² = 25

Take the square root of both sides:

$c = \sqrt {25}$
c = 5 cm

So, the length of the hypotenuse is 5 cm.

Question 2: In a right-angled triangle, the length of the hypotenuse is 13 cm, and one of the other sides measures 5 cm. Find the length of the remaining side.

Solution: Using Pythagoras Theorem (c² = a² + b²), we can determine the length of the remaining side.

Given:

• c = 13 cm
• a = 5 cm

Now, substitute the values into the formula and solve for b:

13² = 5² + b²
169 = 25 + b²
b² = 144

Take the square root of both sides:

$b =\sqrt {144}$
b = 12 cm

So, the length of the remaining side is 12 cm.

Question 3: In a right-angled triangle, the length of the two sides other than hypotenuse are 8 cm and 6cm respectively . Find the length of the hypotenuse.

Solution: Using Pythagoras Theorem (c² = a² + b²), we can determine the length of the hypotenuse.

Given:

• a = 8 cm
• b = 6 cm

Now, substitute the values into the formula and solve for b:

$c^2 = 6^2 + 8^2 = 100$

Take the square root of both sides:

c = 10 cm

Frequently Asked Questions

1. Can Pythagoras Theorem be applied to all types of triangles?

No, Pythagoras Theorem can only be applied to right-angled triangles, where one angle is exactly 90 degrees.

2. How can Pythagoras Theorem help in determining if a triangle is right-angled?

Given the lengths of all three sides of a triangle, you can use the Pythagoras Theorem formula to check if the triangle is right-angled. If the square of the longest side (c) is equal to the sum of the squares of the other two sides (a and b), then the triangle is right-angled.

3. What is the converse of Pythagoras Theorem?

The converse of Pythagoras Theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle.

Related Articles

Pythagorean Triples Formula
Converse of Pythagoras theorem
Similar Triangles Notes