In this article, we will talk about the difference between congruent and similar. Sometimes a math student gets confused between these two terms.
In mathematics, particularly geometry, we use the phrases congruent and similar to compare the shape, proportion, and angles of distinct geometrical figures and shapes.
Congruent vs Similar
The major distinction between congruent and similar shapes is that
Congruent shapes have the same size, and they coincide when superimposed, whereas in the case of similar shapes, they resemble each other but do not have the same exact dimensions, and they never coincide.
Congruent vs Similar
Before going any further and looking at other differences between congruent and similar, let us first define the terms congruence and similarity.
Congruence
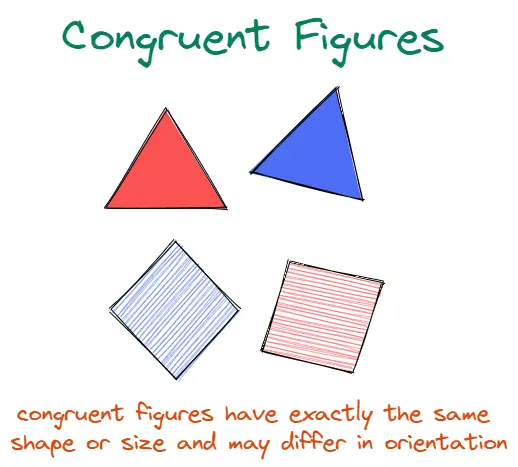
- Congruent shapes have the same dimensions and they overlap when they are superimposed. So, two congruent figures can be mapped exactly to each other.
- These figures can be superimposed on one another despite their differing placements or orientations by simply rotating them till they superimpose together.
- Two congruent objects have the same size and shape but they may differ in their orientation or placement in space.
- Despite having different orientations and placements, they are identical because they have the same dimensions, angles, and other physical characteristics.
Similarity

- Similar figures are ones with a similar shape but different measurements from the other figure used for comparison.
- A mathematical shape, like a circle, for instance, can have a similar basic shape but have a different size.
- Due to their different sizes, these types of figures cannot be superimposed upon one another.
- A similar shape cannot ever be congruent due to the variance in size aspect.
Difference between congruent and similar
Let us look at the difference between these two terms in a tabular form
| Congruent | Similar |
|---|---|
| When two figures or shapes are congruent, they are the same size and shape. | The word "similar" describes objects that have an identical appearance but do not have the same measurements. |
| They can be superimposed upon one another. | They may or may not superimpose on each other. |
| All congruent shapes are similar | All similar shapes are not congruent. |
| The shapes are considered congruent if their angles and side lengths are the same. | In this case, two shapes have proportional corresponding lines and matching angles. They can differ in size. |
| Congruent figures are those that are geometrically precise and superimpose. | Similar refers to figures that are identical in shape. They may or may not ne geometrically precise. |
| Even when placed in different orientations, congruent figures superimpose on each other. This can be accomplished by rotating the figures. | Even when arranged in the same orientation, similar figures do not overlap. |
 Skip to content
Skip to content