Difference Between Log and Ln

logarithms function are important in the study of Maths , Physics and chemistry  We usually express logarithms as log   or ln. Both are widely used in problem and an understanding of the difference between them is important for good score also

Lets find the difference between log and ln

1. Log refers to a logarithm to the base 10 and ln refers to a logarithm to the base e(e = 2.718281828)

$log x = log_{10} x = y$ or $10^y= x$

$ln x = log_{e} x = y$ or $e^y= y$

So , log of number x  is basically  power to which a base of 10 must be raised to obtain a number x

While ln  of number of x is basically  power to which a base of e must be raised to obtain a number x

Here is the table for common values of log

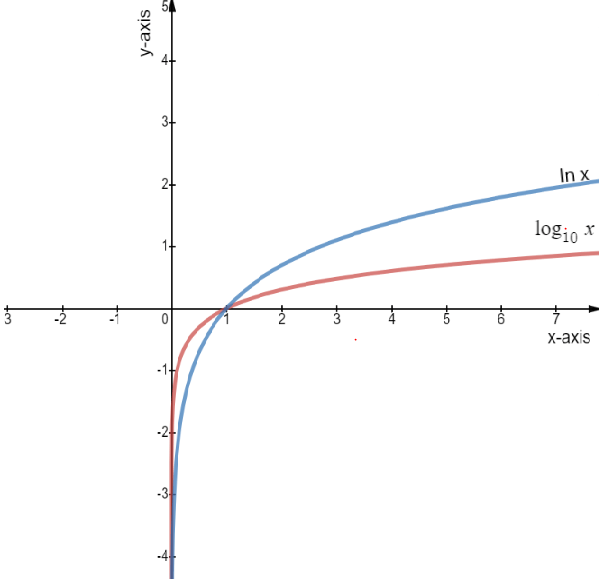
2. The graph of both are shown below

The Relation between log and ln is given by

$ln x = 2.303 log x$

The ln logarithm graph has exactly the same shape as the base 10 logarithm graph; it is just 2.3 times as tall.

3. log is called the  common logarithm while ln is called natural logarithm

4. $log_{10} x$ is usually written as log x . While $log_{e} x$ is usually written as ln x

5. The derivative for ln x is given by

$\frac {d}{dx} [ln x] = \frac {1}{x}$

The derivative for log x is given by

$\frac {d}{dx} [log x] = \frac {1}{x ln 10}$

As per the similarities, the domain of both the log and ln is ${0,-\infty}$ and range is ${\infty,-\infty}$

I hope the difference between log and ln is clear. We need to be very careful while writing these in equation as each denote different thing.

Here we example to practice the values of them

Related Links

1. What is relations?
2. What is Function
3. Domain of Function
4. Range of Function
5. Identity Function
6. Constant Function
7. Linear Function