What is dimension of universal gravitational constant

Dimensional Formula of universal gravitational constant

In this article, we will find the dimension of Universal Gravitational Constant
Dimensional formula for Universal Gravitational Constant is

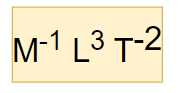
Where
M -> Mass
L-> Length
T -> Time.
We would now derive this dimensional formula.

Derivation for expression of Dimension of Universal Gravitational Constant

The force of gravity between two masses is defined as
$F= \frac {Gm_1m_2}{r^2}$
or
$G= \frac {F r^2}{m_1 m_2}$ -(1)
Where
F -> Force
G ->Universal Gravitational Constant
r -> Distance
m -> Mass

Now Dimension of Mass is $[M^1]$
Dimension of Distance is given by $[L^2]$
Lets derive the dimension of Force
Force is defined as product of Mass and acceleration
$F= m \times a$

Dimension of Mass is given by $[M]$
Dimension of Acceleration is derived as
$a= \frac {dv}{dt}$
Where v = velocity, t= time
Now dimension of Velocity= $[M^0 L^1T^{-1}]$

So Dimension of Acceleration is given by
$\text{Dimension of Acceleration} =\frac {\text{dimension of velocity}}{\text {dimension of time}}$
$\text{Dimension of Acceleration} =\frac { [M^0 L^1T^{-1}] }{[T]}= [M^0L^1T^{-2}]$
Hence Dimension of Force will be
$ \text{Dimension of Force} = [M^1 ] \times [ M^0L^1T^{-2}] = [M^1L^1T^{-2}]$

Now from equation (1) , we can determine the dimension of Universal Gravitational constant as
$ \text{Dimension of G} = \frac { [M^1L^1T^{-2}] \times [L^2]}{[M^2]}$
$=[ M^{-1}L^3T^{-2}] $
Unit of Universal Gravitational constant is m³ kg^?1 s^?2 .

Try the free Quiz given below to check your knowledge of Dimension Analysis:-

---

Quiz on Dimensional Analysis

---

• <<
• 1
• 2
• 3
• 4
• 5
• >>

1. Which of the following physical quantity as the dimension of \([ML^2T^{-3}]\)

impulse

Pressure

Power

Work

Question 1 of 5

2. A dimensionless quantity

always has a unit

does not exist

may have a unit

never has a unit

Question 2 of 5

3. Which of the following has the dimensions of pressure?

\([M^{-1}L^{-1}]\)

\([ML^{-1}T^{-2}]\)

\([MLT^{-2}]\)

\([ML^{-2}T^{-2}]\)

Question 3 of 5

4. A unitless quantity

does not exist

never has nonzero dimensions

always has nonzero dimensions

may have a nonzero dimension

Question 4 of 5

5. The dimensions of universal gravitational constant are

\([M^{-1}L^{3}T^{-2}]\)

\([M^{-2}L^{3}T^{-2}]\)

\([ML^{2}T^{-1}]\)

\([M^{-2}L^{2}T^{-1}]\)

Question 5 of 5

 Loading...

 

---

Related Articles

1. Dimensional Analysis:- a very good website for physics concepts
2. Work Done Formula
3. Work done by Variable Force
4. dimension of Surface Tension
5. Dimension of Momentum

Note to our visitors:-

Thanks for visiting our website.
DISCLOSURE: THIS PAGE MAY CONTAIN AFFILIATE LINKS, MEANING I GET A COMMISSION IF YOU DECIDE TO MAKE A PURCHASE THROUGH MY LINKS, AT NO COST TO YOU. PLEASE READ MY DISCLOSURE FOR MORE INFO.