Summary of electrostatics
This article is about the quick summary of electrostatics for class 12 and iitjee. You can also download electrostatics quick summary PDF if you like and do not forget to share the page so that other people also know about this article on electrostatics summary for class 12 and competitive exams like IITJEE/PMT and all.
In electrostatics we deal with the electric effects of charges at rest.
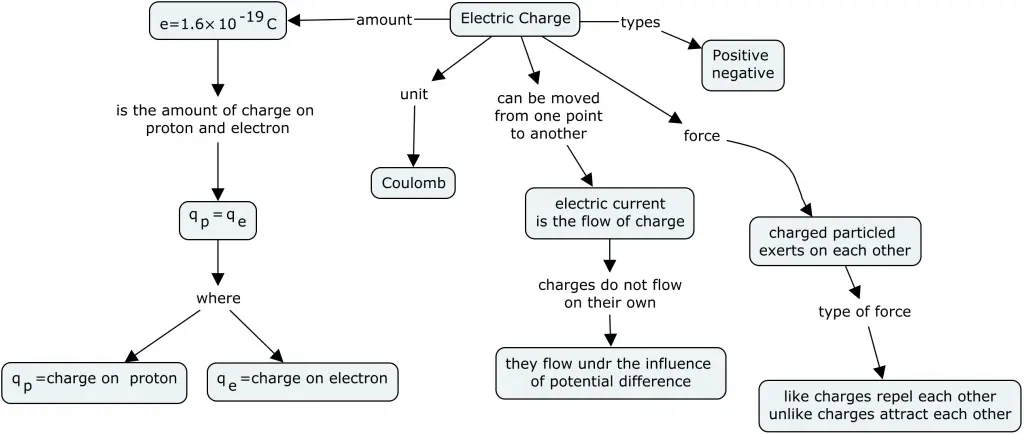
Electric charge can be defined as is the intrinsic characteristic that is associated with fundamental particles due to which they produce and experience electrical and magnetic effects. Charges are of two types
- positive
- negative
The figure given can give you the brief overview of what electric charge is all about
Always note that any material or body in its normal condition is electrically neutral
How to charge a body
A body can be charged either by friction, conduction or by induction
Charging by friction
If we pass a comb through hairs, comb becomes electrically charged and can attract small pieces of paper. Many such solid materials are known which on rubbing attract light objects like light feather, bits of papers, straw etc.
So the phenomenon of production of charges in material or body due to friction ,as in case of above examples, is called frictional electricity.
Charging by conduction
Phenomenon of charge transfer where a charged body is placed in contact with another body so that transfer of electrons takes place from one body to another is called charging by conduction.
Charging by induction
Electrostatic induction is a redistribution of electrical charge in an object, caused by the influence of nearby charges.In the presence of a charged body, an insulated conductor develops a positive charge on one end and a negative charge on the other end.
Properties of electric charge
- Charge is an scalar quantity
- Electric charge is quantized
- Electric charge is additive
- Electric charge is conserved
Conductors allow large scale movement of electric charge through them, insulators do not. In metals the mobile charges are electrons; in electrolytes both positive and negative ions are mobile.
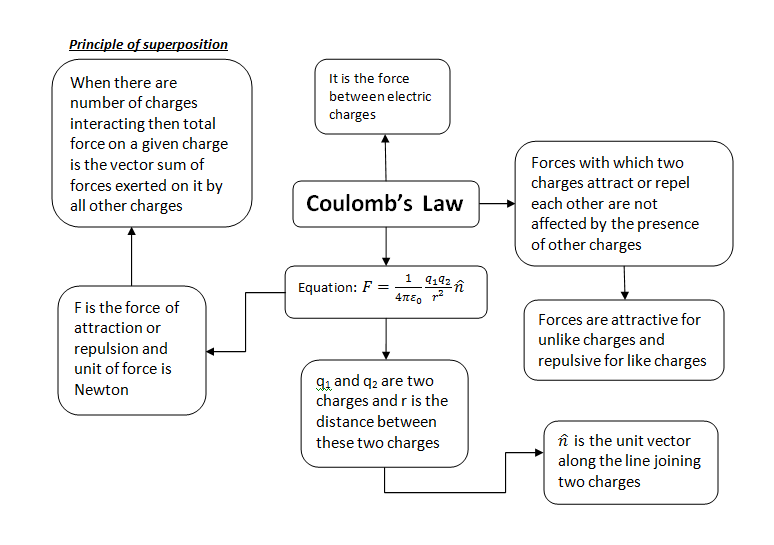
Coulomb’s Law
The electric force exerted on each other by two point charged $q_1$ and $q_2$ , separated by distance $r$, are proportional to the product of $q_{1}q_{2}$, and inversely proportional to the square of the distance between them. they act along the line joining the two charges. These forces are attractive if the charges involved are unlike charges and repulsive if the charges involved are like charges. Mathematically,
$F\propto \frac{q_{1} q_{2}}{r^2}$ or $F=k \frac{q_{1} q_{2}}{r^2}$
Here $k=\frac{1}{4\pi \epsilon_{0}}=8.98755\times 10^{9}Nm^{2}C^{-2}$ is the constant of proportionality.
Electric forces exerted by two charges on each other are equal in magnitude and opposite in direction.
Principle of superposition
Electrostatic force of interaction between two point charges is independent of the presence of other charges.
If a system of charges has n number of charges say q1, q2, ……………….., qn, then total force on charge q1 according to principle of superposition is
F = F12 + F13 + ……………………………. F1n
Where F12 is force on q1 due to q2 and F13 is force on q1 due to q3 and so on.
To have a look at Coulomb’s Law at a glance have a look at the concept map given below
Remember these points
- For each individual pair of charges there is a $\frac{1}{r^2}$ dependence on the separation
- For each pair there is a dependence on the product of charges, with repulsion for like charges and attraction for unlike ones.
- For many charges , the force on any one particular charge can be found as a vector sum by using the superposition principle.
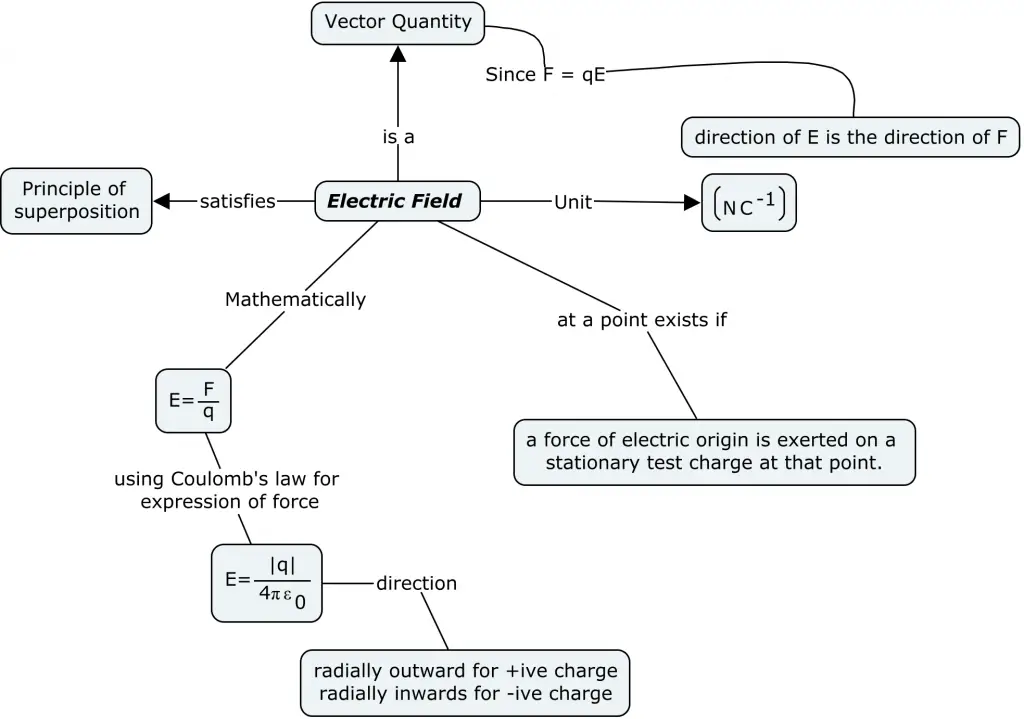
Electrostatic Field
Electric field is the region surrounding an electric charge or a group of charges in which another charged particle experiences a force of attraction or repulsion.
Theoretically electric field extends up to infinity but practically but practically electric field is not detectable beyond a certain distance.
Some Points about Electric field can be revised using the following concept map
It is important to note that:-
- electric field at a point depends only on the sources and not on the test charge. It is a vector sum of contributions one from each source charge.
- An electric field is said to be uniform in a certain region of space if both direction and magnitude of E are same at all points.
- In non uniform field, either the direction or the magnitude or both vary from point to point.
Electric lines of forces
- A line of force is a line drawn in such a way that the tangent at each point on the line gives the direction of electric field at that point
- The relative closeness of lines of forces indicates the strength of electric field at various places.
- They crowd near each other in regions of strong electric field
- They are far apart when the electric field is week.
- In regions of constant electric field , the lines of forces are parallel straight lines.
Important properties of lines of forces
- Line of forces are continuous curves without any break
- Two lines of forces can not cross at common point.
- Lines of forces do not form a closed loop. They start a positive charges and end at negative charges.
- Lines of forces are imaginary
- These lines of forces are so drawn so that their number per unit cross-sectional area in a region is proportional to intensity of electric field.
Electrostatic Potential
Definition:-
In electrostatics electric potential at any point say $P$ is defined as the work done in taking a positive charge from a reference point (generally taken at infinity) to that point $P$ in the presence of electric field.
Important Points
- If $W$ is the work done in taking a point charge $q$ from infinity to point $P$, then electric potential at point $P$ is
$V=\frac{W}{q}$ - Electrostatic potential is a scalar quantity. Its value may be positive or negative.
- If Potential at infinity is chosen to be zero, potential due to a point charge $q$ at the origin is given by
$V=\frac{1}{4\pi \epsilon _{0}}\frac{q}{r}$ - Electric potential at a point due to a given charge distribution is the algebraic sum of the potential due to individual charge.
- Unit of potential is Volt(joul/coulomb)
Potential Difference
- Electric potential difference is the difference of potential between two points.
- The potential difference between two points $A$ and $B$ is work done against electric field in in taking a unit positive charge from $A$ to $B$.
- If $W$ is the work done against electric field in taking the unit positive charge from
$A$ to $B$, $V_{B}-V_{A}=\frac{W}{q}$
and do not consider to forget the signs of both $W$ and $q$. - Potential difference is also a scalar quantity and its unit is Volt
- The electric potential difference due to continuous distribution of charges is given as
$V=\int \frac{1}{4\pi \epsilon _{0}}\frac{dq}{r}$ - Relation between $E$ and $V$ :- Relation between electric field $E$ and potential $V$ is
$dV=-E\cdot dr$
or, $dV=-(E_{x}dx+E_{y}dy+E_{z}dz)$
components of E are related to corresponding derivatives of V in the following manner
$E_{x}=\frac{dV}{dx}$
$E_{y}=\frac{dV}{dy}$
$E_{z}=\frac{dV}{dz}$
Equipotential surfaces
- Surface over which the electric potential is same everywhere is called an equipotential surface.
- Equipotential surfaces are graphical way to represent potential distribution in an electric field.
Electric Potential Energy
Electric potential energy of a test charge at any point in the electric field is the work done against the electric forces to bring the charge from infinity to point under consideration. Mathematically , potential energy of test charge q’ at any distance r from charge q is given by
Full and detailed notes on Electric potential can be read by following this link
Electric field intensity and potential due to different charge distribution
- Due to infinitely long wire:
let $\lambda$ be the charge per unit length of the wire
(a) Field intensity at a distance $r$ from the wire is $E=\frac{\lambda}{2\pi\epsilon_{0}r}$
(b) Electric potential due to infinite wire can not be found but the potential difference between two points is given as $V_B-V_A=-\frac{\lambda}{2\pi\epsilon_{0}}ln\frac{r_{B}}{r_{A}}$ - At a point on axis due to charged ring:-(a) Electric field at any axial point $P$ due to a uniformly charged ring of radius $r$ with charge $q$ is given as
$E=\frac{qx}{4\pi\epsilon_{0}\left ( x^{2} +r^{2}\right )^{\frac{3}{2}}}$
where $x$ is the distance of point $P$ from the center of the ring. Electric field is directed away from the ring if it is positively charged and towards it if it is negatively charged.
(b) Electric potential at this point $P$ would be
$V=\frac{q}{4\pi\epsilon{0}\sqrt{x^{2}+r^{2}}}$
(c) From above equations we can conclude that at the center electric field $E=0$ and $V=\frac{q}{4\pi\epsilon_{0}r}$ which is maximum value for potential .Electric field intensity is maximum when $x=\pm \frac{r}{\sqrt{2}}$ it is
$E_{max}=\frac{1}{4\pi \epsilon _{0}}\sqrt{\frac{3}{2}}\cdot \frac{q}{r^{2}}$
also the field intensity and electric potential both are zero at infinity . - At the center of the half ring:-
If $\lambda$ is the charge per unit length on the half ring of radius $r$ then electric field intensity at center of the ring would be
$E=\frac{\lambda}{2\pi\epsilon_{0}r}$
and electric potential at center of the half ring would be
$V=\frac{\lambda}{4\epsilon_{0}}$ - Uniformly charged disk:-
If $q$ is the total amount of charge on a disk of radius $R$ then surface charge density of the disk would be$\sigma=\frac{q}{\pi R^{2}}$let $r$ be the distance of the point $P$ on the axis from the center of the disk then electric field intensity at point $P$ would be$E=\frac{\sigma}{2\epsilon_{0}}\left [ 1-\frac{r}{\sqrt{r^{2}-R^{2}}} \right ]$Its direction will be along the axis. For positively charged particles , it would be away from the disk and for negatively charged it is towards the disk.Now electric potential at point P will be$V=\frac{\sigma}{2\epsilon_{0}}\left [ \sqrt{r^{2}-R^{2}} – r^{2} \right ]$From above two equations we can conclude that- for very close point $r<<R$:
$E=\frac{\sigma}{2\epsilon_{0}}$
$V=\frac{\sigma R}{2\epsilon_{0}}$
- for very close point $r<<R$:
Electric Dipole:
Electric dipole is a set of two equal and opposite charges that are separated by small finite distance.
If $2a$ is the distance between two charges $+q$ and $-q$ then electric dipole moment is given as
$\vec{p}=2q\vec{a}$
Electric field due to dipole
On axis of the dipole
$E_{axis}=\frac{1}{4\pi\epsilon_{0}}\frac{2p}{r^{3}}$
direction would be along the direction of dipole moment.
$V=\frac{1}{4\pi\epsilon_{0}}\frac{p}{r^{2}}$
On equatorial point
$E_{equitorial}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{r^{3}}$
Direction would be opposite to the direction of dipole moment and potential would be zero.
Torque on a dipole in an external field
$\tau =\vec{p}\times \vec{E}$
potential energy of a dipole in an electrostatic field
$U=-\vec{p}\cdot\vec{E}$
Gauss’s Law
It states that total electric flux through a closed surface is equal to $\frac{1}{\epsilon_{0}}$ times the net charge $q$ enclosed by the surface i.e.,
$\int \vec{E} \cdot d\vec{s}=\frac{q}{\epsilon_{0}}$
where $d\vec{s}$ is an element of area; the direction of each element $d\vec{s}$ of $\vec{s}$ is along the outward drawn normal to the surface at every point.
- It is the net charge enclosed in the surface that matters in Gauss’s law but the total flux of electric field E depends also on the surface chosen not merely on the charge enclosed.
- So if you have information about distribution of electric charge inside the surface you can find electric flux through that surface using Gauss’s Law.
- Again if you have information regarding electric flux through any closed surface then total charge enclosed by that surface can also be easily calculated using Gauss’s Law.
- Surface on which Gauss’s Law is applied is known as Gaussian surface which need not be a real surface.
- Gaussian surface can be an imaginary geometrical surface which might be empty space or it could be partially or fully embedded in a solid body.
For more notes and study material on Gauss’s Law you can visit this link and follow on from there.
Capacitance
I have already made a pdf document on the summary of this chapter and I will be providing the download link below.
For more detailed notes on capacitance follow this link
 Skip to content
Skip to content
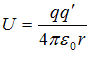
Thanks for these notes
How this create this page…..i thanks a lot
thank you
How can I get full pdf note of electrostatic
Please visit
Class 12 physics notes
and there you can find electrostatics notes.