Stable unstable and neutral equilibrium Questions for JEE Examination

What is Equilibrium

A rigid body is supposed to be in equilibrium if there is no change in translational motion and no change in rotational motion
General conditions for equilibrium are as follows
(i) The total force must be zero
(ii) The total torque about any axis must be zero.
Sometimes it is convenient to consider torques about axes through the center of gravity.

Types of equilibrium

We can divide the equilibrium into two categories  with respect to the state of a body
1. Static equilibrium.
2. Dynamic equilibrium.

Static equilibrium
If the total force and total torque on the body are zero and the body is in the state of rest then its equilibrium is termed as static equilibrium.
For example All stationary bodies

Dynamic equilibrium
when a body is in a state of uniform motion and the resultant total force and total torque on the body are zero then it is said to be in dynamic equilibrium.

STABLE, UNSTABLE AND NEUTRAL EQUILIBRIUM

Stable Equilibrium: A body is in stable equilibrium if it comes back to its normal position on slight displacement

Examples
(1) A ball in the valley between two hills. a small displacement of the ball toward either side will result in a force returning the ball to the original position. Thus the equilibrium is stable

(2)A book lying on a horizontal surface is an example of stable equilibrium. If the book is lifted from one edge and then allowed to fall, it will come back to its original position

(3) A cone with a flat surface on the horizontal floor. If the cone is tilted slightly, it comes back to its normal position

Neutral equilibrium: If a ball is pushed slightly to roll, it will neither come back to its original nor it will roll forward rather it will remain at rest.

Examples:
(1) A ball on a flat surface. A small displacement will not have any impact on the ball.

Unstable equilibrium: A body is in unstable equilibrium if it does comes back to its normal position on slight displacement

Example
(1) pencil standing on its point or a stick in vertically standing position.

(2) thin rod standing vertically is slightly disturbed from its position it will not come back to its original position.

(3) Vertically standing cylinder

(4) A ball at the top of a rounded hill.A small displacement of the ball results in a force that moves the ball away from the equilibrium point so that equilibrium cannot be maintained.

Important notes about Equilibrium

(1) The position of the center of gravity of an object affects its stability. The lower the center of gravity (G) is, the more stable the object. The higher it is the more likely the object is to topple over if it is pushed.

(2) The body always tries to go to the lowest point for the center of gravity. So if the center of gravity is tilted above on displacement from the equilibrium position, then the body will come back to the lowest point. So equilibrium would be stable. if the center of gravity is tilted below on displacement from the equilibrium position, then the body will not come back to the normal position. So equilibrium would be unstable. This looks to be very clear from the example ball in the valley

(3)  We will need to find the direction of the force on the body when slightly displaced to find out if the equilibrium is stable, unstable, or neutral.  If the force is restoring i,e direction is towards the equilibrium position then it is a stable equilibrium. if the force is away i,e direction is away from the equilibrium position then it is an unstable equilibrium. If no force acting then neutral equilibrium

Equilibrium And Potential energy

If only conservative forces are acting on the system, then we can define equilibrium in terms of Potential energy also

For 1D motion, we can write it like

$dU = -F_{x}dx$

Now For equilibrium, Force should be zero
Then
$F_{x}=-\frac{dU}{dx}=0$

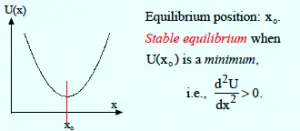
For stable equilibrium, the second derivative should be positive. So for slight displacement, the restoring force should act on the body

$\frac {d^{2}U}{dx^{2}}  > 0$

potential energy diagram for the Stable Equilibrium

For unstable equilibrium, the second derivative should be Negative. So for slight displacement, the force should take away the body from the equilibrium position

$\frac {d^{2}U}{dx^{2}}  < 0$

potential energy diagram for the Unstable Equilibrium

For Neutral equilibrium, the second derivative should be zero. So for slight displacement, There is no force

$\frac{d^{2}U}{dx^{2}}  = 0$

potential energy diagram for the Neutral Equilibrium

We can see lots of these examples  in gravitational PE, Spring PE, and electrical PE

How to solve the Potential energy function equilibrium Problems

(1) Potential energy function must be given for the problem
(2) Differentiate with respect to the variable
(3) To find the equilibrium points, put dU/dx=0  and solve for the values of x
(4) Perform second differentiation of the Potential energy function
(5) Find the value of the second derivative for the equilibrium points
(6) If it is positive, we are having stable
(If it is zero, it is neutral equilibrium
(if it is negative ,it is unstable equilibrium

Solved Examples

(1) The potential energy function of the object confined to move along x-axis  x> 0 is given below
$U(x)=U_{0}[(\frac{k}{x})^{12}-2(\frac{k}{x})^{6}]$
Here k > 0  and $U_{0}$ > 0

Find the equilibrium position and find out if it is stable,neutral and unstable equilibrium?

Solution

Now

$U(x)=U_{0}[(\frac{k}{x})^{12}-2(\frac{k}{x})^{6}]$

Differentiating with respect to x

$\frac{dU}{dx}=U_{0}[-12\frac{k^{12}}{x^{13}}+12\frac{k_{6}}{x^{7}}]$
Now for equilibrium position,
$\frac{dU}{dx}=0$
$U_{0}[-12\frac{k^{12}}{x^{13}}+12\frac{k_{6}}{x^{7}}]=0$
or x=k

Again Differentiating with respect to x

$\frac{d^{2}U}{dx^{2}}=U_{0}[+156\frac{k^{12}}{x^{14}}-84\frac{k_{6}}{x^{8}}]$

Now for x=k
We get

$\frac{d^{2}U}{dx^{2}}=72\frac{U_{0}}{k^{2}}$

Which is clearly positive as  k > 0  and $U_{0}$ > 0
So it is the case of Stable equilibrium

(2)  The potential energy U of an object of unit mass in a one-dimensional conservative force field is given by

U=x²-4x+3.

(a)Find out the equilibrium position and if the object will perform SHM on little displacement from the equilibrium position.

(b) Find the Time period  of the motion

(c) If the speed of the object at equilibrium position is 4m/s,what is the amplitude of the oscillations

Solution

U=x²-4x+3.

$F=-\frac{dU}{dx} =-(2x-4)$

At equilibrium Position ,force is zero

So -(2x-4) =0 or x=2 m is the equilibrium position

Let the object is displaced with x₀ from equilibrium position,then force

F=-2[(x₀  +2)-4]= -2x₀

So Force is directly proportional to displacement and it is restoring one also. So object will execute SHM about equilibrium Position

$\text{Time period(T)} =2 \pi \sqrt{\frac{m}{k}}$

$T =2 \pi \sqrt{\frac{1}{2}} = \sqrt {2} \pi sec$

Now for finding the amplitude, we will use energy conservation

Total energy at Equilibrium position =Total energy at Extreme point

KE + U_min= U_max

$\frac {m*v^2}{2} + U_{min}= U_{max}$

$8 + [2^2 -4 \times 2 +3]=(A+2)^2 -4(A+2) +3$

Solving this for A

A=2$ \sqrt {2}$ m

(3) A particle of mass m is present in a region where the potential energy of the particle depends on x-coordinate and it is given by the expression

$U= \frac{a}{x^2} – \frac {b}{x}$

(a)Find out the equilibrium position and if the object will perform SHM on little displacement from the equilibrium position.

(b) Find the Time period  of the motion

Solution

$U= \frac{a}{x^2} – \frac {b}{x}$

$F=-\frac{dU}{dx} =- [ \frac {-2a}{x^3} + \frac {b}{x^2}]$

At equilibrium Position F=0

$- [ \frac {-2a}{x^3} + \frac {b}{x^2}]=0$

or $x_0=\frac {2a}{b}$

For little displacement  $x=x_0 + \Delta x$, Force will be given by

$F=-[\frac {bx-2a}{x^3}] = -[\frac {b(x_0+\Delta x) -2a}{(x_0+\Delta x)^3} =-\frac {b\Delta x}{(x_0+\Delta x)^3}$

Now as $\Delta x <<< x_0$

$F=-\frac {b\Delta x}{x_0^3}=-\frac {b^4}{8a^3} \Delta x$

Since F is directly proportional to $\Delta x$, this is SHM

Time period is given by

$\text{Time period(T)} =2 \pi \sqrt{\frac{m}{k}}$

$T =2 \pi \sqrt{\frac{8a^3 m}{b^4}}$

Hope this post on Stable unstable and neutral equilibrium is helpful for students .Please do provide the feedback

Also Reads
Work Done by Multiple Forces
How to solve Kinematics Problems
Force Given Potential Energy
https://en.wikipedia.org/wiki/Mechanical_equilibrium
Physics Formulas