How to find work done by Multiple forces acting on a object

Many times in a problem we have multiple forces acting on the body and we need to calculate work done by Multiple force. This can be done in these simple steps

(1) First draw a free body diagram of the body showing all the forces on it.

(2) Carefully choose a X-Y coordinate system so that  direction of the motion  or direction of force lies in X or Y direction. This will simplify the Problem

(3) Applying Newton’s law find out any unknown forces

(4) Find the work done by individual forces using the formula

$W= \mathbf{F}.\mathbf{d}$
The work done is the scalar product of the Force and displacement vector
This can be written as
$W=Fd \cos \theta $

And net Workdone will be the Sum of the workdone of the individual forces

$W=W_{1}+W_{2}+W_{3}$

Another way would be to first find the net Force on the object ( Vector Sum)

$\mathbf{F}_{net}=\mathbf{F}_{1}+\mathbf{F}_{2}+\mathbf{F}_{3}$

And then

$W= \mathbf{F}_{net} .\mathbf{d}$
$W_{net}=F_{net}d \cos \theta$

(5) The Work done can also be calculated using the  Scalar dot product if the forces and displacement vectors are given

W= F.d

(6) All the above steps are applicable  if the force acting is constant,if the force is  of varying nature,then it becomes little bit complicated to find out

(a)  The force in a spring depends on the distance from the equilibrium position,so it is of varying nature.In such a case,following could be used to calculate the work done

$W=\int_{a}^{b}f_{x}xdx$

where  $f_{x}x$ is the force varies  with x.

This could also be calculated using the graphical method. It is the area of the curve plotted between force component parallel to displacement between the two points

Example -1

A block moves up an inclined plane of 30° under the action of the three forces shown in the below figure
$F_3= 40 N$ and horizontal direction
$F_1=10 N$ and Normal to the plane
$F_2=30 N$ and parallel to the plane
Determine the work done by each of these forces and net work done as the block moves up 100 cm the incline

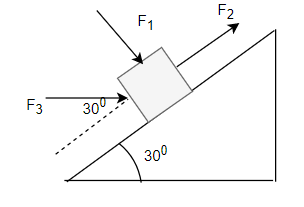
Solution
Work done by the Force $F_3$ is given by
$W_3 = F_3 d \cos \theta$
$=10 \times 1 \times .866= 8.66$ J

Work done by the Force $F_1$ is given by
$W_1 = F_1 d \cos \theta$
$=10 \times 1 \times 0= 0$ J
Since force act perpendicular to the direction of movement. Work done is zero

Work done by the Force $F_2$ is given by
$W_2= F_2 d \cos \theta$
$=30 \times 1 \times 1= 30 $ J

Hence Net work done= $W_1 + W_2 + W_3 = 0 + 30 + 8.66= 38.66 $J

Example 2
A 10 kg box is pulled on the rough horizontal floor at a constant speed of 20 cm/s by a horizontal force. The coefficient of friction between the block and floor is .20.
(a) Find the work done by pulling force per second
(b) Find the work done by the friction force per second
(c) Net work done on the box

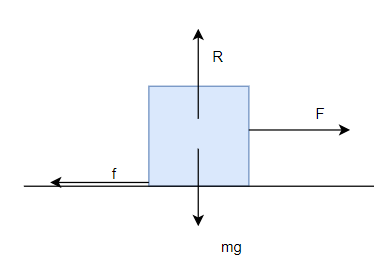
Solution:
Since the speed is constant
$\mathbf{F}= \mathbf{f}$
Now
$f= \mu mg= .30 \times 10 \times 9.8 = 29.4 $N
Therefore $F= 29.4 $N
Now displacement in 1 sec(d) = 20 cm = .2 m
(a) Work done by the Pulling Force
$W_1 = Fd= 29.4 \times .2= 5.88$J
(b) Work done by the Friction Force
$W_2 = -fd= -29.4 \times .2= -5.88$J ( Negative sign as friction is opposite to direction of movement)
(c) Net work done
$W= W_1 + W_2 = 0$

I hope you like this post on How to find work done by Multiple forces acting on a object

Also Reads
calculate force from potential energy
physics formulas
work done Formula
how to solve kinematics problems