Number 64 is a composite number and we will find how to find the factors of 64. We will also see techniques to find out the Prime factorization of 64 easily
Factors of 64
A factor of a number is an exact divisor of that number. So factors of 64 are the numbers which are exact divisors of 64.
Factors of any number can be found by finding the number which divides the number without remainder, or alternatively, numbers that can multiply together to equal the target number being converted
Let us check how to find the factors
Method -1
Factors can be found by finding the numbers which when multiplied together give the number 64. Now to find the numbers we can start with the integer 1 and keep increasing it by 1 and we will discard where the other number cannot be found. We will stop at a point where we start seeing the repetition of numbers We will find the multiplication one by one and start writing it down. So
$64 = 1 \times 64$
$64= 2 \times 32 $
$64 = 4 \times 16 $
$64= 8 \times 8 $
$64= 16 \times 4 $
Since 4 and 16 are repeated, we stop here
So factors are 1,64,2,32,4,16,8
Putting the factors in ascending order, we get
1,2,4,8,16,32,64
Method -2
Factors can be found by finding the numbers which divide the number without a remainder. We can start with the following sequence: 1,2,3,4… and go till the mid-point of that number.
No Remainder
$64/2 = 32$ . No Remainder
$64/4 = 16$. No remainder
$64/8 =8$. No remainder
$64/16 =4$. No remainder
$64/32 =4$. No remainder
$64/64 =1$. No remainder
So factors are 1,2,4,8,16,32,64
Hence Factors of 64 are 1,2,4,8,16,32,64
prime factorization of 64
When a number is expressed as a product of its factors we say that the number has been factorized. When the factorization contains the prime number only then it is called prime factorization.
Now let us look at how to find the prime factorization
There are two methods that can be used.
Division method
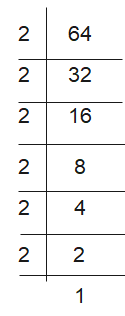
We divide the number 64 by 2, 3,4,5,6,7, etc. in this order repeatedly so long as the quotient is divisible by that number.
Thus, the prime factorization is $ 2 \times 2 \times 2 \times 2 \times 2 \times 2$ or $2^6$
Factor Tree Method
In this method, we first think about any two factors, and then we think about two factors of respective numbers. This goes till the factors are prime.
We can have many factor trees depending on the starting point but all of them will show the same prime factors.
Let’s check the different Factor trees for number 64

Hence the Prime Factorization is $2^6 $
Factor of 64 in pair
We can find the factors of number 64 in pairs, by multiplying two numbers in a pair to get the original number as 64, such as:
$64 = 1 \times 64$
$64= 2 \times 32 $
$64 = 4 \times 16 $
$64= 8 \times 8 $
So factor in pair are (1,64) , (2,32), (4,16), (8,8)
Hope you like the post
Also Reads
 Skip to content
Skip to content