Here in this post, learn how to draw the graph of cosec inverse cosec x($csc^{-1}(csc(x))$) step-by-step with clear instructions and examples in this comprehensive guide.
Here, we will understand how to draw the graph of cosec inverse cosec x i.e
$f(x) = cosec^{-1} cosec (x)$
As $cosec (2\pi +x ) = cosec x$
This is a periodic function with period $2\pi$
Also, x cannot take values like $n\pi$ as undefined
When you apply $ (\csc^{-1}) to (\csc(x))$, you are essentially asking, “What is the angle whose cosecant is the cosecant of x?” In a perfect mathematical world without any restrictions, $(\csc^{-1}(\csc(x)))$ would simply be (x). However, due to the defined ranges of inverse trigonometric functions, this is true only if (x) is within the principal value range of $(\csc^{-1}).$
As we take the principal value range of $(\csc^{-1})$ as $([-\frac{\pi}{2}, \frac{\pi}{2}])$ excluding 0, then $(\csc^{-1}(\csc(x)) = x)$ only if (x) is in that range. If (x) is outside that range, the expression will not simply return (x), but rather an equivalent angle within the principal value range.
Therefore by definition
$f(x) = cosec^{-1} cosec (x) = x $ if $x \in (-\pi/2, \pi/2) – {0}$
Let’s check out the other values
if $x \in (\pi/2, 3\pi/2] – {\pi}$
$\pi/2 < x \leq 3\pi/2 $
$ – 3\pi/2 \leq -x < -\pi/2$
Adding $\pi$
$ -\pi/2 \leq \pi – x < \pi/2 $
Also $cosec (\pi -x) = cosec x$
So $f(x) = cosec^{-1} cosec (x) = cosec^{-1} cosec ( \pi – x)= \pi -x$
here $ x \ne \pi$
if $x \in (3\pi/2, 2\pi)$
$3\pi/2 < x < 2\pi $
subtracting $2\pi$
$ -\pi/2 < x -2 \pi < 0 $
Also $cosec (2\pi -x) = -cosec x$
or $ -cosec (x -2 \pi) = -cosec x$
or $cosec (x-2 \pi)= cosec x$
So $f(x) = cosec^{-1} cosec (x) = cosec^{-1} cosec ( x -2 \pi)= x – 2\pi$
here $ x \ne 2\pi$
In Short
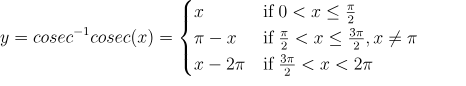
Therefore the graph of cosec inverse cosec x will be
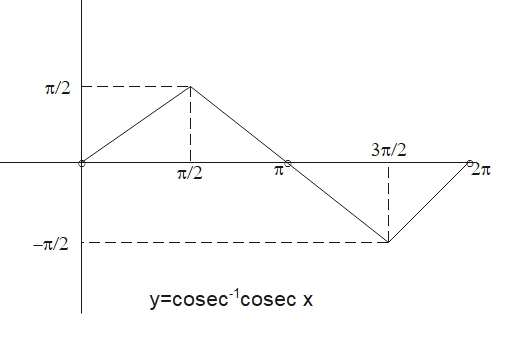
I hope the concept is clear. Please comment if you don’t understand any concept
