Integration of odd function

The integration of odd function over a symmetric interval can be understood through some fundamental concepts in calculus and symmetry. An odd function is defined as a function $f(x)$ that satisfies the condition $f(-x) = -f(x)$ for all $x$ in the domain of the function. Graphically, odd functions exhibit symmetry about the origin, meaning their graphs are invariant under a rotation of 180 degrees around the origin.

When integrating an odd function over a symmetric interval $[-a, a]$, the result is always zero. This outcome can be intuitively understood by considering the symmetry of odd functions: for every positive value of $x$ that contributes a certain area under the function curve between $0$ and $a$, there is a corresponding negative value of $x$ between $-a$ and $0$ whose contribution to the integral cancels out the positive area, due to the nature of odd functions.

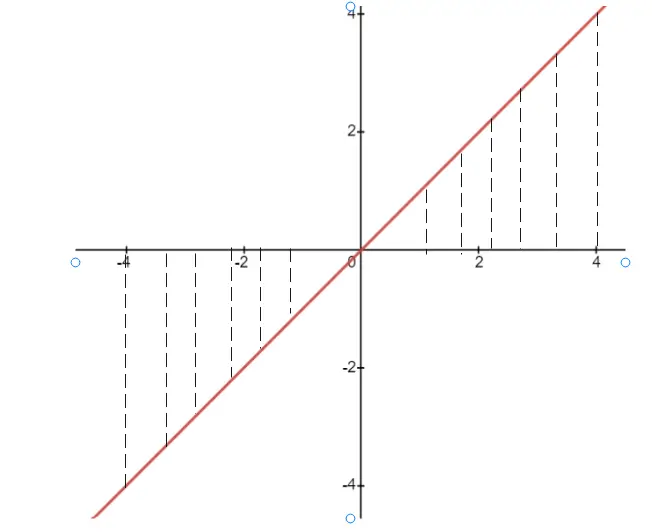
Let f(x) =x and it is a odd function and we can clearly see that the area of the curve in the left half plane is equal to the area of the curve in the right half plane but they are opposite sign and hence they cancel out

Mathematically, this property can be shown using the definition of the definite integral:

$$
\int_{-a}^{a} f(x)\,dx = 0 \quad \text{for odd functions } f(x).
$$

Proof of this Integral

$$
\int_{-a}^{a} f(x)\,dx = \int_{-a}^{0} f(x)\,dx + \int_{0}^{a} f(x)\,dx.
$$

For the first integral, we can perform a variable substitution $u = -x$, which transforms the integral as follows:

$$
\int_{-a}^{0} f(x)\,dx = \int_{a}^{0} f(-u)(-du) = \int_{0}^{a} -f(u)\,du,
$$

where we have used the fact that $f(-u) = -f(u)$ because $f$ is odd, and $-du$ is due to the change of variable ($dx = -du$). This shows that the area under the curve from $-a$ to $0$ is the negative of the area from $0$ to $a$, leading to their sum being zero:

$$
\int_{0}^{a} f(x)\,dx + \int_{0}^{a} -f(x)\,dx = 0.
$$

Example 1:

Integration of $f(x) = x^3$ over $[-2, 2]$

Solution

Now
$f(x) = x^3$
$f(-x) = (-x)^3 = -x^3$
So,
($f(-x) = -f(x)$).
which is an odd function
Therefoe

$$
\int_{-2}^{2} x^3\,dx =0
$$

Example 2:

$$
\int_{-1}^{1} (5x^5 – 3x^3)\,dx
$$

Solution

Now
$f(x) = 5x^5 – 3x^3$
$f(-x) = -5x^5 +3x^3= -(5x^5 – 3x^3)$
So,
($f(-x) = -f(x)$).
which is an odd function
Therefre

$$
\int_{-1}^{1} (5x^5 – 3x^3)\,dx=0
$$

Important Properties

If f(x ) and g(x) are two odd function, then their sum and subtraction will also be odd function, so

$$
\int_{-a}^{a} (f(x) + g(x)) \,dx = 0
$$

$$
\int_{-a}^{a} (f(x) – g(x)) \,dx = 0
$$

If f(x ) and g(x) are two odd function, then their product and division will be even function

$$
\int_{-a}^{a} (f(x) g(x)) \,dx = 2 \int_{0}^{a} (f(x) g(x)) \,dx
$$

$$
\int_{-a}^{a} (f(x) /g(x)) \,dx = 2 \int_{0}^{a} (f(x) /g(x)) \,dx
$$

Solved Questions

Question 1

$
\int_{-1}^{1} \frac {x^3}{x^2 + 2|x| +1} \, dx
$

Solution
$f(x) = \frac {x^3}{x^2 + 2|x| +1}$

$f(-x) = \frac {-x^3}{x^2 + 2|x| +1} = -f(x) $
which is an odd function
Therefre
$
\int_{-1}^{1} \frac {x^3}{x^2 + 2|x| +1} \, dx =0
$

Question 2

$
\int_{-1}^{1} \ln \frac {10 -x}{10 + x} \, dx
$

Solution
$f(x) = \ln \frac {10 -x}{10 + x} )

$f(-x) = \ln \frac {10 +x}{10 – x} $
$=\ln (10 +x ) – \ln (10-x) = -( \ln (10-x) – \ln (10 +x )) = – \ln \frac {10 -x}{10 + x}= -f(x)
which is an odd function
Therefore
$
\int_{-1}^{1} \ln \frac {10 -x}{10 + x} \, dx =0
$

Hope you like this article on Integration of odd function. Please do provide the feedback