Trigonometric table from 0 to 360 (cos -sin-cot-tan-sec-cosec)

Trigonometric ratios are important module in Maths. Here in this post, I will provide Trigonometric table from 0 to 360 (cos -sin-cot-tan-sec-cosec) and also the easy and simple way to remember it.

Trigonometric table for 0 to 90 is given by

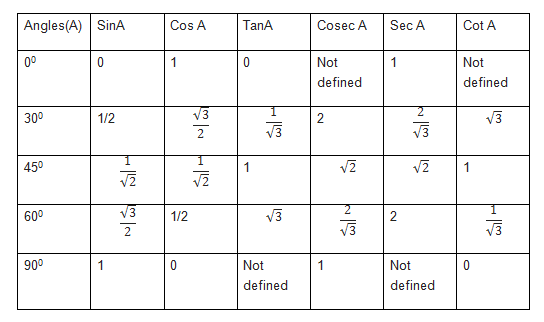
And this can be easily remember by below method

How to easily remember trigonometric ratios table

Trigonometric table(sin-cos-tan table) for 0 to 360 is given by

Now to remember the Trigonometric table for 120 to 360 , we just to need to remember sign of the functions in the four quadrant. We can use below phrase to remember

ALL SILVER TEA CUPS

ALL  –  All the trigonometric function are positive in Ist Quadrant

SILVER – sin and cosec  function are positive ,rest are negative in II Quadrant

T EA – tan and cot function are positive, rest are negative in III Quadrant

CUPS – cos and sec function are positive , rest are negative in IV quadrant

Now we can use  the formula in below table to calculate the ratios from 120 to 360

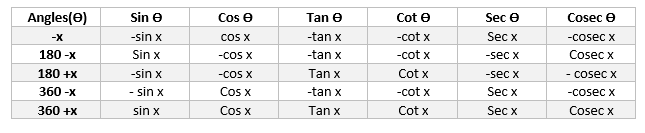
This table is very easy to remember, as each correspond to same function.The sign is decided by the corresponding sign of the trigonometric function of the angle in the quadrant

For example

a. $ \cos 120 = \cos (180 -60) = – \cos 60$  . It is easy to remember and sign is decided by the angle quadrant. Since 120 lies in II quadrant ,cos is negative

b.$\sin 120 = \cos (180 -60) = \sin 60$. Here since sin is positive in II quadrant, we put positive sign

c. $\tan 120 = \tan (180 -60) = – \tan 60$. Here since tan is negative in II quadrant, we put negative sign

Now Trigonometric table for 120 to 180 is given by

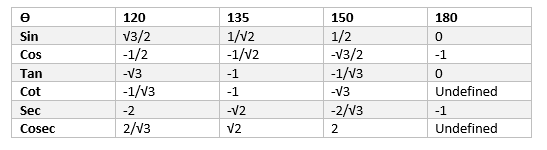
And it is calculated as

$\sin (120) = \sin (180 -60) =\sin 60= \frac {\sqrt {3}}{2}$

$\cos (120) = \cos (180 -60) =- \cos 60= – \frac {1}{2}$

$\tan 120 = \frac {\sin 120}{\cos 120} = -\sqrt {3}$

$\sin (135) = \sin (180 -45) = \sin 45= \frac {1}{\sqrt {2}}$

$\cos (135) = \cos (180 -45) =- \cos 45= -\frac {1}{\sqrt {2}}$

$\tan 135 = \frac {\sin 135}{ \cos 135} = -1$

$\sin (180) = \sin (180 -0) =sin 0= 0$

$\cos (180) = \cos (180 -0) =-cos 0= -1$

$\tan 180 = \frac {\sin 180}{\cos 180} = 0$

$\csc 120 = \frac {1}{\sin 120} = \frac {2}{\sqrt 3}$

$\sec 120 = \frac {1}{\cos 120} = -2$

$\cot 120 = \frac {1}{\tan 120} = – \frac {1}{\sqrt 3}$

$\csc 135 = \frac {1}{\sin 135} = \sqrt 2$

$\sec 135 = \frac {1}{\cos 135} = -\sqrt 2$

$\cot 135 = \frac {1}{\tan 135} = – 1$

Now Trigonometric table for 210 to 270 is given by

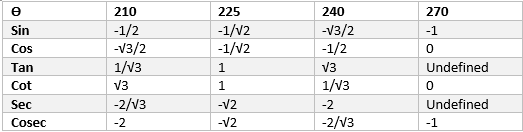
And it is calculated as

$\sin (210) = \sin (180 +30) =- \sin 30= -\frac {1}{2}$

$\cos (210) = \cos (180 +30) =- \cos 30=-\frac {\sqrt {3}}{2}$

$\tan (210) = \frac {\sin 210}{ \cos 210} = \frac {1}{\sqrt {3}}$

$\sin (225) = \sin (180 +45) =- \sin 45= -\frac {1}{\sqrt {2}}$

$\cos (225) = \cos (180+45) =- \cos 45= -\frac {1}{\sqrt {2}}$

$\tan 225 = \frac {\sin 225}{\cos 225} = 1$

$\sin (270) = \sin (180 +90) =- \sin 90= -1$

$\cos (270) = \cos (180+90) =- \cos 90= 0$

$\tan 270 = \frac {\sin 270}{\cos 270} = -\frac {1}{0}$ Undefined value

$\csc (210) = \frac {1}{\sin (210)} = -2$

$\sec (210) = \frac {1}{\cos (210)}=-\frac {2}{\sqrt 3}$

$\cot (210) = \frac {1}{\tan (210)} = \sqrt {3}$

$\csc (225) = \frac {1}{\sin 225}= -\sqrt {2}$

$\sec (225) = \frac {1}{\cos 225}= -\sqrt {2}$

$\cot 225 = \frac {1}{\tan 225} = 1$

Now Trigonometric table for 300 to 360 is given by

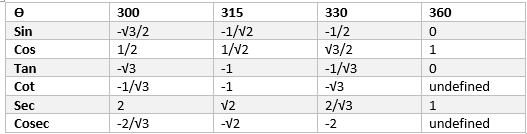
$\sin (300) = \sin (360 -60) =- \sin 60=-\frac {\sqrt {3}}{2}$

$\cos (300) = \cos (360-60) =\cos 60=\frac {1}{2}$

$\tan (300) = \frac {\sin 300}{\cos 300} = -{\sqrt {3}}$

$\sin (315) = \sin (360 -45) =- \sin 45= -\frac {1}{\sqrt {2}}$

$\cos (315) = \cos (360-45) =\cos 45= \frac {1}{\sqrt {2}}$

$\tan 315 = \frac {\sin 315}{ \cos 315} =- 1$

$\sin (360) = \sin (360 -0) =- \sin 0=0$

$\cos (360) = \cos (360-0) =\cos 0=1$

$\tan (360) = \frac {\sin 360}{\cos 360} = 0$

$\csc (300) = \frac {1}{\sin (300)}=-\frac {2}{\sqrt 3}$

$\sec (300) = \frac {1}{\cos (300)}=2$

$\cot (300) = \frac {1}{\tan 300} = -\frac {1}{\sqrt {3}}$

How to calculate the trigonometric ratios of negative of the   angle from 0 to 360

This is quite simple.Just remember this single thing

$\cos( x) = \cos (-x)$  and $\sec(x) = \sec(-x)$

For rest all ratios

$\sin (x) = – \sin(-x)$ , $\csc (x) = – \csc (-x)$

$\tan (x) = – \tan (-x)$ , $\cot (x) = – \cot(-x)$

So we can find negative of any angle as

$\cos (-120) = \cos (120) = \cos (180 -60) =- \cos 60 = -\frac {1}{2}$

$\sin (-120)= – \sin(120) = – \sin 60 = – \frac {\sqrt {3}}{2}$

We have explained everything is terms of degrees, same thing can be done in radian form also

Related Posts

Trigonometric functions
Domain ,Range and Graphs of Trigonometric functions
Trigonometric equations
trigonometry formulas for class 11
Sin 15 degrees
Sin 18 degrees
https://en.wikipedia.org/wiki/Trigonometry