Find the Values of Sin 15, cos 15 ,tan 15 ,sin 75, cos 75 ,tan 75

Values of Sin 15, cos 15 ,tan 15  ,sin 75, cos 75 ,tan 75 of degrees can be easily find out using the trigonometric identities.  Also there can be many ways to find out the values. Lets explore few ways

Value of sin 15 degrees

Method 1 ( using sin 30)

$(\sin \frac {A}{2} + \cos \frac {A}{2} )^2 = \sin^2 \frac {A}{2} + \cos^2 \frac {A}{2} + 2 \sin \frac {A}{2} \cos \frac {A}{2} $

Now $\sin^2 \frac {A}{2} + \cos^2 \frac {A}{2} $

and  $\sin A= 2 \sin \frac {A}{2} \cos \frac {A}{2}$

Therefore

$(\sin \frac {A}{2} + \cos \frac {A}{2} )^2 = 1 + \sin A$

$\sin \frac {A}{2} + \cos \frac {A}{2} =\pm \sqrt {1 + \sin A}$

Similarly

$(\sin \frac {A}{2} – \cos \frac {A}{2} )^2 = \sin^2 \frac {A}{2} + \cos^2 \frac {A}{2} – 2 \sin \frac {A}{2} \cos \frac {A}{2} $

or

$\sin \frac {A}{2} – \cos \frac {A}{2} =\pm \sqrt {1 – sin A}$

Now putting A= 30, we get

$\sin 15 + \cos 15 = \pm \sqrt {1 + sin 30}$

and

$\sin 15 – \cos 15 = \pm \sqrt {1 – sin 30}$

Now we know that sin 15 > 0 and cos 15 > 0,

Therefore

$\sin 15 + \cos 15 =  \sqrt {1 + \sin 30}  = \frac {\sqrt {3}}{\sqrt {2}}$ -(1)

But we are not sure about the values of sin 15 – cos 15

Lets see how to determine it

$\sin 15 – \cos 15 = \sqrt {2} ( \frac {1}{\sqrt 2} sin 15 – \frac {1}{\sqrt 2} \cos 15)$

$=\sqrt {2} (\cos 45 \sin 15 – \sin 45 \cos 15) = \sqrt {2} \sin (15 -45) = – \sqrt {2} \sin 30$

So it is a negative

$\sin 15 – \cos 15 = – \sqrt {1 – \sin 30} = – \frac {1}{ \sqrt {2}}$ -(2)

Adding (1) and (2), we get

$2 \sin 15 = \frac {\sqrt {3}}{\sqrt {2}} – \frac {1}{ \sqrt {2}}$

$\sin 15 = \frac {\sqrt {3} -1}{2\sqrt {2}}$

Method -2 (using 45 and 60 values)

$\sin 15 = \sin (60 -45)$

$\sin (A -B) = \sin A \cos B – \cos A \sin B$

$= \sin 60 \cos 45 – \cos 60 \sin 45$

$= \frac {\sqrt {3}}{2} \frac {1}{\sqrt {2}} – \frac {1}{2}  \frac {1}{\sqrt {2}} $

$\sin 15 = \frac {\sqrt {3} -1}{2\sqrt {2}}$

Value of cos 15 degrees

Subtracting (2) from (1), wet get

$2 \cos 15 = \frac {\sqrt {3}}{\sqrt {2}} +  \frac {1}{ \sqrt {2}}$

$\cos 15 = \frac {\sqrt {3} +1}{2\sqrt {2}}$

Method 2

$\cos 15 = \cos (60 -45)$

$\cos(A – B) = \cos A  \cos B + \sin A \sin B$

$= \cos 60 \cos 45  + \sin 60 \sin 45$

$=\frac {\sqrt {3} +1}{2\sqrt {2}}$

Value of tan 15 degrees

Now

$\tan 15 = \frac {\sin 15}{\cos 15} $

$= \frac {\sqrt {3} -1}{\sqrt {3} +1}$

Value of sin 75 degrees

$\sin 75 = \sin (90 -15) =\cos 15$

$\sin 75= \frac {\sqrt {3} +1}{2\sqrt {2}}$

Value of cos 75 degrees

$\cos 75 = \cos (90 -15) =\sin 15$

$\cos 75= \frac {\sqrt {3} -1}{2\sqrt {2}}$

Value of tan 75 degrees

Now

$\tan 75 = \frac {\sin 75}{\cos 75} $

$= \frac {\sqrt {3} +1}{\sqrt {3} -1}$

Summary

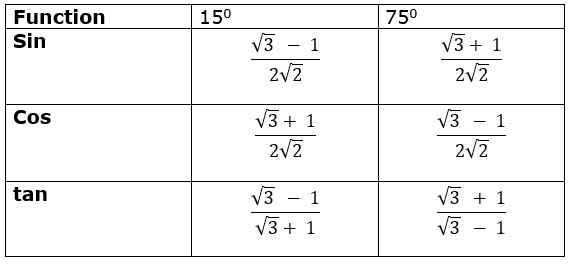
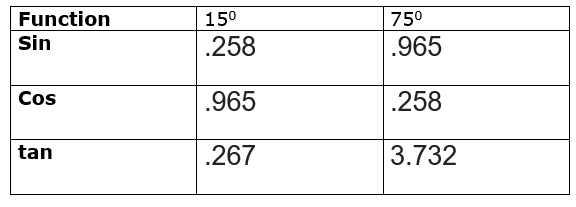
In decimals

Related Articles

sin cos tan table
sin 18 degrees
Trigonometry Formulas for class 11 (PDF download)
Inverse Trigonometric Function Formulas
Integration Formulas

---