What is the dimension of Voltage

Dimensional Formula of Voltage

with its Derivation

In this article, we will find the dimension of Voltage

Dimensional formula for Voltage is

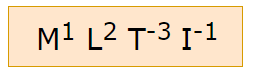
Where

M -> Mass

L -> Length

T -> Time

I -> Current

We would now derive this dimensional formula.

Derivation for expression of Dimension of Voltage

Derivation of Voltage can be done with any formula which contains voltage

A. Voltage is defined as Work done per unit Charge

$V= \frac {W}{q} $

Now $W = f \times d$

Dimension of Force = $[M^1 L^1 T^{-2}]$

Dimension of distance = $[L^1]$

So, Dimension of Work done is =$[M^1 L^1 T^{-2}] \times [L^1]=[M^1 L^2 T^{-2}]$

Now charge is given as

$q = I \times t$

Hence Dimension of charge is $[I^1 T^1]$

Now that we know the dimension of work done and charge, dimension of Voltage will be given by

$=\frac {[M^1 L^2 T^{-2}]}{ [I^1 T^1]} = [M^1 L^2 T^{-3} I^{-1}]$

B. Voltage is also defined as

$V= E \times d$

Where E is the electric Field

Now Electric Field is defined as

$E= \frac {F}{q}$

Dimension of Force= $[M^1 L^1 T^{-2}]$

Dimension of charge is $[I^1 T^1]$

So dimension of E = $\frac {[M^1 L^1 T^{-2}]}{[I^1 T^1]}= [M^1 L^1 T^{-3} I^{-1}]$

Hence Dimension of Voltage is given by

$=[M^1 L^1 T^{-3} I^{-1}] \times [L^1]=[M^1 L^2 T^{-3} I^{-1}]$

Unit of Voltage is Volt

Try the free Quiz given below to check your knowledge of Dimension Analysis:-

---

Quiz on Dimensional Analysis

---

• <<
• 1
• 2
• 3
• 4
• 5
• >>

1. The dimension of torque is

\([MLT^{-2}]\)

\([ML^2T^{-2}]\)

\([ML^3T^{-3}]\)

\([ML^{-1}T^{-1}]\)

Question 1 of 5

2. Which of the following has the dimensions of pressure?

\([MLT^{-2}]\)

\([ML^{-1}T^{-2}]\)

\([M^{-1}L^{-1}]\)

\([ML^{-2}T^{-2}]\)

Question 2 of 5

3. The dimensions of universal gravitational constant are

\([ML^{2}T^{-1}]\)

\([M^{-1}L^{3}T^{-2}]\)

\([M^{-2}L^{3}T^{-2}]\)

\([M^{-2}L^{2}T^{-1}]\)

Question 3 of 5

4. The dimensions of impulse are equal to that of

linear momentum

pressure

angular momentum

force

Question 4 of 5

5. Which of the following pair does not have similar dimensions

stress and pressure

angle and strain

tension and surface tension

Planck's Constant and angular momentum

Question 5 of 5

 Loading...

 

---

Related Articles

1. https://physicscatalyst.com/elec/coulombs-law.php :- visit this page to know more about Coulomb’s law and dielectric constant or relative permittivity.
2. New Simplified Physics by SL Arora : I highly recommend this book for class 11 Physics students. It is easy to understand with lots of solved problems.
3. Dimensional Analysis:- a very good website for physics concepts
4. dimension of frequency
5. Dimension of permittivity in Vacuum
6. dimension of Resistance

Note to our visitors:-

Thanks for visiting our website.
DISCLOSURE: THIS PAGE MAY CONTAIN AFFILIATE LINKS, MEANING I GET A COMMISSION IF YOU DECIDE TO MAKE A PURCHASE THROUGH MY LINKS, AT NO COST TO YOU. PLEASE READ MY DISCLOSURE FOR MORE INFO.