Extra Questions for Area of parallelograms & triangles

Given below is Area of parallelogram worksheet
a. Concepts questions
b. Calculation problems
c. Multiple choice questions
d. Long answer questions
e. Fill in the blank's

Short Answer Type

Question 1
Which of the following figures lie on the same base and between the same parallels?
In such a case, write the common base and the two parallel


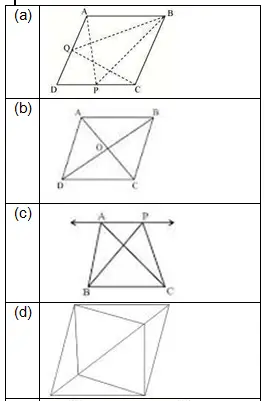
Solution
a. True.  With Base BC and between parallel AD and BC, Triangle QBC and parallelogram ABCD
b. True. With base DC or AB and between parallel DC and AB, triangles are present
c. True. Same as above
d. False
e. True. Same as a
f. False
g. True

True and False

Question 2
True or False statement
(a) If two triangles area are same areas, they will be congruent
(b) Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
(c) The area of a triangle is equal to the product of any of its side and any altitude
(d) The median of the triangles divides the triangle into two triangles of equal areas
(e) Parallelograms on the same base and between same parallels have same perimeter
(f) In a parallelogram, diagonals divide the parallelogram into four equal triangles
Solution

1. False. Congruent triangles have equal areas but converse is not true
2. True.  Triangle area is (1/) X base X height. With same base and area, height should be equivalent, which means they lie on same parallel
3. False. It is corresponding base and corresponding altitude
4. True. 
5. False. Area is same but perimeter can be different
6. True

Question 3
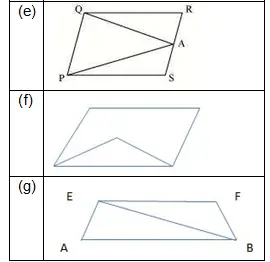
PQRS is a rectangle with O as any point in its interior. If area (ΔPOS)= 4 cm² and area(ΔQOR)= 6 cm², then area of rectangle PQRS
(a) 10cm²
(b) 20cm²
(c) 14 cm²
(d) 15²
Solution
Answer is (b)
$\frac{1}{2}PS \times (alitude)_{1}=4cm^{2}$
$\frac{1}{2}QR \times (alitude)_{2}=6cm^{2}$
Now PS=QR, So adding
$\frac{1}{2}PS \times [(alitude)_{1}+(altitude)_{2}]=10cm^{2}$
Now altitude₁ + altitude₂= PQ=RS
So area of rectangle=20 cm²

Question 4
In the below figure AD is the median, And E is any point on AD

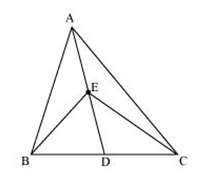
Which of the following is true?
(a) Area of triangle AEB= Area of triangle AEC
(b) Area of triangle DEB= Area of triangle DEC
(c)Area of triangle ABD= Area of triangle ADC
(d) All the above
Solution
Answer is (d)
Since AD is median, it bisect the triangle is equal areas
So Area of triangle ABD= Area of triangle ADC    ---(1)
Now ED is the median for EBC triangle
So Area of triangle DEB= Area of triangle DEC   --(2)
Subtracting 1 and 2, we get
Area of triangle AEB= Area of triangle AEC

Question 5
In the given figure ABCD is a parallelogram   AE ⊥ DC and   CF ⊥ AD. If AB = 18 cm, AE = 8 cm and CF = 16 cm, find AD.

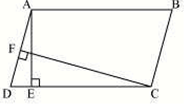
(a) 9 cm
(b) 8 cm
(c) 10 cm
(d) None of the above
Solution
Answer is (a)
Parallelogram area= base X height
So DC×AE=AD×CF
Or AD=DC×AE/CF=9 cm

Question 6
In the below figure AD is the median, and E is mid-point on AD. If the area of triangle is 16 cm², what is the area of the triangle BED

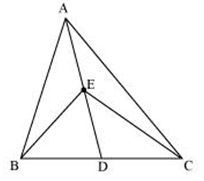
(a) 3cm²
(b) 4cm²
(c) 5 cm²
(d) None of these
Solution
Answer is (b)

Question 7
PQRS is a quadrilateral whose diagonal bisect each other at right angles
(a) PQRS is a Square
(b) PQRS is a rectangle
(c) PQRS is a rhombus
(d) None of these
Solution
answer is (c)

Question 8
In a quadrilateral ABCD, diagonal BD and AC intersect at point X

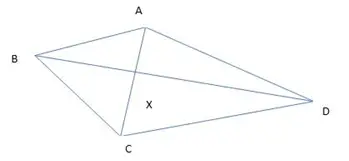
Which of the following is true?
(a) (Area of triangle BXC)×( Area of triangle AXD)=( Area of triangle AXB)×(Area of triangle CXD)
(b) (Area of triangle BXC)+( Area of triangle AXD)=( Area of triangle AXB)+(Area of triangle        CXD)
(c) Insufficient information
(d) None of these
Solution
Answer is (a)
Hint, Draw perpendicular from A and C on BD and the calculate the area of each these piece and arranged them to get the solution

Question 9
Two parallelograms are on the same base and between the same parellels. The ratio of their areas is:
(a) 1:2
(b) 1:1
(c) 1:4
(d) None of these
Solution
Answer is (b)

Question 10
In a triangle A,B,C,D and E are such point BD=DE=EC

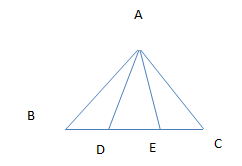
Which of the following is true?
(a) Area of triangle ABD=Area of triangle ADE=Area of triangle AEC
(b) Area of triangle ADE=(1/3) Area of triangle ABC
(c) Triangle ABD is congruent to triangle AEC
(d) None of the above
Solution
Answer is (a), (b)
Hint: Draw perpendicular from A on BC and then calculate area for each of these triangle and you will find it same

Match the column

Area of the triangle is 20 cm2, Area of rectangle is	25cm2.
Area of the parallelogram is 100 cm2. Both the Diagonal are drawn which cut the area into four pieces. The area of each piece is	40cm2
In a triangle ABC,all the median intersect at point G, If the area of the triangle is 150 cm2,what is the area of the triangle AGC	10 cm2
A trapezoid as parallel sides of 4 and 6 cm respectively, The altitude is 5 cm.A diagonal is drawn which cut the trapezoid into two traingles.Area of the triangle with base 4 cm is	50 cm2

Solution
(a) 40 cm²
(b) 25cm²
(c) 50 cm²
(d) 10 cm²

Summary

This Class 9 Maths Important Questions for Area of parallelograms & triangles with answers is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail.