Inverse Trigonometric Function Formulas

---

Inverse Trigonometric Function Formulas

---

Inverse Trigonometric Functions are important topic in Trigonometry. Here is detailed list of Inverse Trigonometric Function Formulas

Domain and Range Of Inverse Trigonometric Functions

The value of an inverse trigonometric functions which lies in its principal value branch is called the principal value of that inverse trigonometric functions

Graph of Inverse Trigonometric Functions

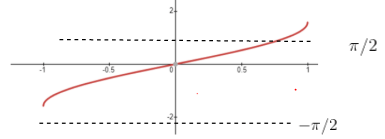
$sin^{-1} x$

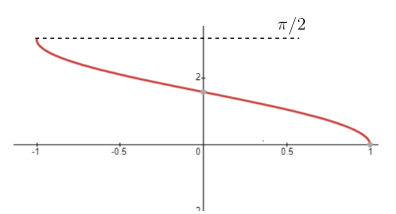
$cos^{-1} x$

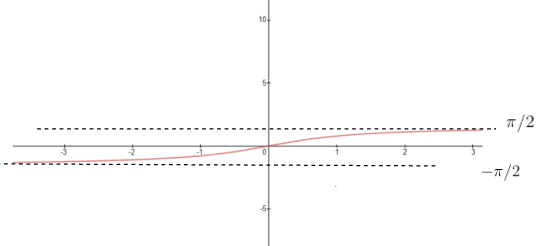
$tan^{-1} x$

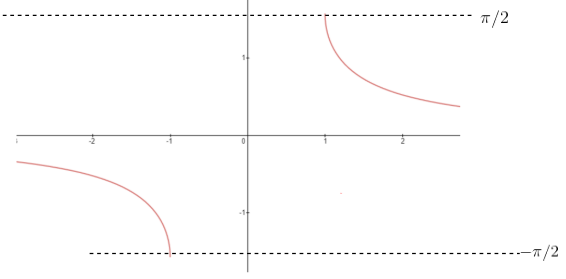
$cosec^{-1} x$

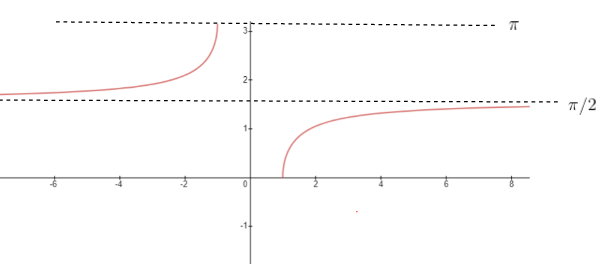
$ sec^{-1} x$

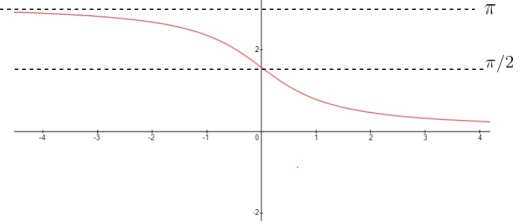
$cot^{-1} x$

More Formulas

$sin (sin^{-1} x) = x$ and $sin^{-1} (sin \theta) = \theta$, if $- \frac {\pi}{2} \leq \theta \leq \frac {\pi}{2}$ and $- 1 \leq x \leq 1$.
$cos (cos^{-1} x) = x$ and $cos^{-1} (cos \theta) = \theta $, if $0 \leq \theta \leq \pi$ and $- 1 \leq x \leq 1$
$tan (tan^{-1} x) = x$ and $tan^{-1} (tan \theta) = \theta $ if $- \frac {\pi}{2} \leq \theta \leq \frac {\pi}{2}$ and $ – \infty < x < \infty$.
$cosec (cosec^{-1} x) = x$ and $cosec^{-1} (cosec \theta) = \theta$ if $- \frac {\pi}{2} \leq \theta < 0$ , $ 0 < \theta \leq \frac {\pi}{2}$ and $- \infty < x \leq -1$ or $1 \leq x < \infty$ .
$sec (sec^{-1} x) = x$ and $sec^{-1} (sec \theta) = \theta$ if $0 \leq \theta < \frac {\pi}{2}$ or $\frac {\pi}{2} < \theta \leq \pi $ and $- \infty < x \leq -1$ or $1 \leq x < \infty$.
$cot (cot^{-1} x) = x$ and $cot^{-1} (cot \theta) = \theta$, if $0 < \theta < \pi$ and $ – \infty < x < \infty$

Inverse of Negative x

$sin^{-1} (-x) = -sin^{-1} (x)$
$cos^{-1} (-x) = \pi – cos^{-1} (x)$
$tan^{-1} (-x) = -tan^{-1} (x)$
$sec^{-1} (-x) = \pi – sec^{-1} (x)$
$cosec^{-1} (-x) = -cosec^{-1} (x)$
$cot^{-1} (-x) = \pi – cot^{-1} (x)$

Other Formulas

$sin^{-1} (\frac {1}{x}) = cosec^{-1} (x)$
$cos^{-1} (\frac {1}{x}) = sec^{-1} (x)$
$tan^{-1} (\frac {1}{x}) = cot^{-1} (x)$
$sin^{-1} (x) + cos^ {-1} (x) = \frac {\pi}{2}$
$sec^{-1} (x) + cosec^ {-1} (x) = \frac {\pi}{2}$
$tan^{-1} (x) + cot^ {-1} (x) = \frac {\pi}{2}$
$sin^{-1} (x) + sin^ {-1} (y) = sin ^{-1} (x \sqrt {1-y^2} + y \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 \leq 1$
$sin^{-1} (x) + sin^ {-1} (y) = \pi – sin ^{-1} (x \sqrt {1-y^2} + y \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 > 1$
$sin^{-1} (x) – sin^ {-1} (y) = sin ^{-1} (x \sqrt {1-y^2} – y \sqrt {1-x^2)}$ if $x,y \geq 0 $, $x^2 + y^2 \leq 1$
$sin^{-1} (x) – sin^ {-1} (y) = \pi – sin ^{-1} (x \sqrt {1-y^2} – y \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 > 1$
$cos^{-1} (x) + cos^ {-1} (y) = cos ^{-1} (x y – \sqrt {1-y^2} \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 \leq 1$
$cos^{-1} (x) + cos^ {-1} (y) = \pi – cos ^{-1} ((x y – \sqrt {1-y^2} \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 > 1$
$cos^{-1} (x) – cos^ {-1} (y) = cos ^{-1} (x y + \sqrt {1-y^2} \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 \leq 1$
$cos^{-1} (x) – cos^ {-1} (y) = \pi – cos ^{-1} (x y + \sqrt {1-y^2} \sqrt {1-x^2})$ if $x,y \geq 0 $, $x^2 + y^2 > 1$
$tan^{-1} (x) + tan^ {-1} (y)= tan^{-1} (\frac {x+y}{1-xy})$ , if $x,y > 0 $, $xy < 1$
$tan^{-1} (x) + tan^ {-1} (y)= \pi + tan^{-1} (\frac {x+y}{1-xy})$ , if $x,y > 0 $, $xy > 1$
$tan^{-1} (x) + tan^ {-1} (y)= tan^{-1} (\frac {x+y}{1-xy}) – \pi$ , if $x < 0, y > 0 $, $xy > 1$
$tan^{-1} (x) – tan^ {-1} (y)= tan^{-1} (\frac {x-y}{1+xy}) – \pi$ , if $xy > -1$
$tan^{-1} (x) + tan^ {-1} (y) + tan^ {-1} (z) = tan^{-1} (\frac {x+y+z – xyz}{1-xy-yz-xz})$
$ 2 sin^{-1} (x) = sin^{-1} (2x \sqrt {1-x^2})$ if $ -\frac {1}{\sqrt {2}} \leq x \frac {1}{\sqrt {2}} $
$ 2 cos^{-1} (x) = cos^{-1} (2x^2 -1)$
$2 tan^{-1} (x) = tan^{-1} (\frac {2x}{1-x^2})$ if $ -1 <x < 1$
$2 tan^{-1} (x) = sin^{-1} (\frac {2x}{1+x^2})$ if $ |x| \leq 1$
$2 tan^{-1} (x) = cos^{-1} (\frac {1 -x^2}{1+x^2})$ if $ x \geq 0$
$3 sin^{-1} (x) = sin^{-1} (3x -4x^3)$
$3 cos^{-1} (x) = cos^{-1} (4x^3 – 3x)$
$3 tan^{-1} (x) = tan^{-1} (\frac {3x -x^3}{1-3x^2})$

Inverse trigonometric functions are very useful in a wide range of applications. Understanding these functions is crucial for solving problems in mathematics, physics, and engineering. By mastering the properties and identities of inverse trigonometric functions, you can gain a deeper understanding of trigonometry and its applications.

---

Related Articles

Trigonometry Formulas for class 11 (PDF download)
sin cos tan table
Integration Formulas
sin 18 degrees
tan 15 degrees
Differentiation formulas
https://en.wikipedia.org/wiki/Differentiation

---