Motion In a Straight Line class 11 Notes

In this article, you will get revision notes for topic motion in a straight line class 11 notes for physics NCERT book chapter 3. It is important to note here that motion in a straight line is nothing but motion in one dimension. Such a type of motion is also called linear motion or rectilinear motion.

Motion in a Straight Line Notes Physics Chapter 3

These Motion In a Straight Line notes can also be used if you are preparing for competitive exams like NEET, JEE Mains and JEE Advanced. We also have topic-wise notes on class 11 physics where you can have notes, worksheets etc for free.

Motion in a straight line notes for neet and IIT JEE

What is Kinematics

Kinematics as we all know is the study of physical bodies (or objects) in motion without getting into the causes of that motion.
Kinematics is the study of physical quantities such as distance, displacement, speed, velocity, and acceleration.

Introduction

When we look around, we see various moving objects, such as people walking, automobiles driving, Ferris wheels spinning, etc.
Everything in the universe is in motion, from Earth orbiting the Sun to the moon revolving around Earth.
Change in the position of an object over time is defined as motion in physics.
Both rest and motion are relative concepts.
A body that is moving relative to one reference system may be at rest with respect to another frame of reference.

Point Object

In the field of kinematics, the term point object is often used.
A moving object might be considered a point object if it is very small compared to the distance it covers.
Examples of point objects:-
(a) A car that travels 10 kilometres can be considered a “point object.”
(b) When studying how the Earth orbits the Sun, it can be viewed as a point.

Position, Distance and Displacement

Position

When we talk about a particle’s position, we mean where it is in space at a certain point in time.
To represent the position of a moving object at any particular time, we require a coordinate system with three mutually perpendicular axes.
This coordinate system can be attached to the frame of reference of our choice.
The position of a particle can be defined with respect to this frame of reference.

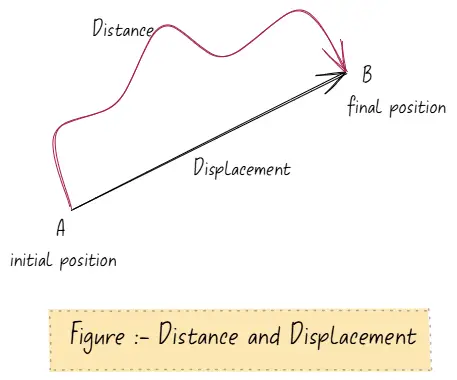
Distance

Distance is the total path length travelled by the moving object.
It is the total length of the path travelled between two positions.
It is a scalar quantity that only has magnitude but no direction
SI unit for measurement of distance is a meter.

Displacement

The displacement of an object is the change in its position.
It is the shortest distance between the object’s initial and final positions in a given direction.
Meter is the SI unit for displacement.
Displacement has both direction and magnitude. So it is a vector quantity.
Its magnitude can never be greater than the total distance i.e. |Displacement|\leq Distance
Distance and displacement are equivalent if a particle moves in a straight line without changing direction.
It can be positive, negative or zero.

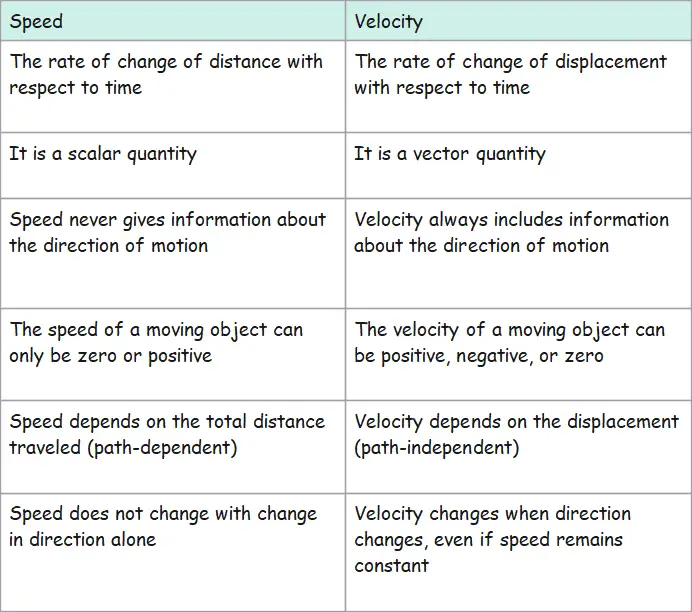
Speed

The speed of a moving object is defined as the total distance covered divided by the time taken to cover that distance.
$$\text{Speed}=\frac{\text{Total Distance Covered}}{\text{Time Taken}}$$
Unit of speed – In the SI system speed is measured in $m/s$. Sometimes $Km/hr$ or mile per hour $(mph)$ is also used to express speed.
Dimensional Formula – $[M^0LT^{-1}]$
The speed of an object can be positive or zero. It can not be negative.
It is a scalar quantity.

Uniform Speed

An object has constant speed if it traverses an equal distance in equal time intervals, however small these time intervals may be.

Variable Speed

An object is considered to be moving at a variable speed if it travels the same distance in unequal time intervals, no matter how small these time intervals are.

Average Speed

How fast an object moves
It is defined as the total distance covered divided by the time taken to cover that distance $$\text{Average Speed}=\frac{\text{Total Distance Covered}}{\text{Time Taken}}=\frac{\Delta x}{\Delta t}$$
Calculated when an object moves with variable speed.

Instantaneous speed

An object moving with variable speed has different values of speed at different instances of time.
The instantaneous speed of an object is the speed of an object at a given instant of time.
A car’s speedometer gives us instantaneous speed.

Velocity

How fast an object moves and in what direction.
The velocity of an object is defined as the displacement divided by the time it takes for the displacement. Mathematically, $$Velocity=\frac{Displacement}{Time}$$

Unit of velocity- In the SI system velocity is measured in m/s. Sometimes Km/hr or mile per hour (mph) is also used to express velocity.
Its direction is the same as that of displacement.
Dimensional Formula – $[M^0LT^{-1}]$
The velocity of an object can be positive, negative or zero.
It is a vector quantity.

Uniform Velocity

An object is said to move with uniform velocity if it covers equal displacements in equal time intervals, no matter how small these time intervals are.
Here both magnitude of velocity as well as the direction of velocity remains constant.

Variable Velocity

A body is said to have had variable or non-uniform velocity if it covers unequal displacement in equal intervals of time. however small these time intervals may be.
In this case, the magnitude of displacement, the direction of motion, or both change as time passes.
Example:-
A body moving in a circle at a constant speed has a non-uniform velocity. This is because, even if the magnitude of the velocity remains constant, the direction of the body’s velocity changes.

Average Velocity

It is defined as the total displacement covered divided by the time taken for that displacement $$\text{Average Velocity}=\frac{\text{Displacement}}{\text{Time Taken}} or, \bar v=\frac{\Delta \vec x}{\Delta t}$$
The bar over v indicates average velocity.
Calculated when an object moves with variable velocity.

Instantaneous Velocity

The velocity of a particle at a particular instant of time is given by instantaneous velocity.
Instantaneous velocity is also known as the limit of average velocity as the time interval becomes infinitesimally small. Mathematically instantaneous velocity, $$v=\lim_{\Delta\rightarrow0}\frac{\Delta x}{\Delta t}$$
The limit of ratio $\frac{\Delta x}{\Delta t}$ as $\Delta t$ approaches zero is called the derivative of $x$ with respect to $t$ and is written as $dx/dt$

Acceleration

The rate of change of velocity is called acceleration.
The change in velocity can be in either the magnitude or the direction of the velocity, or both at the same time.
Mathematically,$$acceleration\; \vec a=\frac{\vec v}{t}$$
Like velocity, acceleration is a vector quantity.
Acceleration can be negative or positive and can be zero.
Negative acceleration is also known as deceleration or retardation.
Uniform acceleration occurs when an object undergoes equal changes in velocity at equal time intervals.
SI unit of acceleration is $m/s^2$
The dimensional formula of acceleration is $[M^0L^1T^{-2}]$

Average Acceleration

The change in velocity divided by the time interval is defined as the average acceleration over that time interval.
It is an average change of velocity per unit of time.
Mathematically, $$a=\frac{v_2-v_1}{t_2-t_1}$$ where, $v_2$ is velocity at time $t_2$ and $v_1$ is velocity at time $t_1$.

Instantaneous Acceleration

The acceleration of a particle at a particular instant of time is given by instantaneous acceleration.
It is also known as the limit of average acceleration as the time interval becomes infinitesimally small. Mathematically,$$a=\lim_{\Delta\rightarrow0}\frac{\Delta v}{\Delta t}=\frac{dv}{dt}$$
The limit of ratio $\frac{\Delta x}{\Delta t}$ as $\Delta t$ approaches zero is called the derivative of $x$ with respect to $t$ and is written as $dv/dt$
In the case of uniform acceleration, instantaneous acceleration equals average acceleration over that time period.

Equations of Motion

If the particle’s velocity changes at a constant rate, this rate of change of velocity with time is referred to as the constant acceleration.
Equations of motion link an object’s displacement to its velocity, acceleration, and time.
Although an object’s motion can take many different trajectories but here we will concentrate on motion in a straight line (or motion in one dimension).
We can have positive and negative displacement, velocity, and acceleration. Negative quantities point in the opposite direction as positive quantities.
The following equations are for motion with constant acceleration $a$, initial velocity $u$, and final velocity $v$. The acceleration happens over time $t$, and the displacement from the original position is $s$.

Motion In a Straight Line class 11 Notes

Motion under gravity

Free Fall

In the absence of air resistance, all bodies fall with the same acceleration near the surface of the earth.
This motion of a body falling towards the earth from a small height is called free fall.
The acceleration with which the body falls is called acceleration due to gravity and is denoted by $g$. ($g=9.8m/s^2$ near the surface of the earth)

Free Fall Equations of motion

Following are the equations of motion for a freely falling body:
1. $v=u+gt$
2. $s=ut+\frac{1}{2}gt^2$
3. $v^2-u^2=2gs$
When a body falls freely under the action of gravity, its velocity increases and the value of g is taken as positive.
When a body is thrown vertically upward, its velocity decreases and the value of g is taken as negative.
For a body thrown vertically upward with initial velocity u, we have
- Maximum Height reached : $h=\frac{u^2}{2g}$
- Time of ascent = Time of descent $=\frac{u}{g}$
- Total time of flight to come back to the point of projection $=\frac{2u}{g}$
- The velocity of fall at the point of projection $=u$
- Velocity attained by the body dropped through height$h$, $v=\sqrt{2gh}$

Relative Velocity

The relative velocity of object A with respect to object B is defined as the rate at which its (object A) position changes with respect to object B.
Mathematically, if $\vec{v}_A$ and $\vec{v}_B$ are the velocities of object A and B respectively then the relative velocity of A with respect to B is defined as $$\vec{v}_{AB}=\vec{v}_A-\vec{v}_B$$
Relative velocity of object B w.r.t. to object A $$\vec{v}_{BA}=\vec{v}_B-\vec{v}_A$$
The relative velocity of two objects moving in the same direction is equal to the difference in their speeds i.e., $$\vec{v}_{AB}=\vec{v}_A-\vec{v}_B$$
The relative velocity of two moving objects in opposite directions is the sum of their speeds i.e., $$\vec{v}_{AB}=\vec{v}_A+\vec{v}_B$$
When $\vec{v}_A and \vec{v}_B$ are inclined to each other at an angle $\theta$, $$ \vec{v}_{AB}=\sqrt{v_A^2+v_B^2-2v_Av_B\cos\theta}$$
If $\vec{v}_{AB}$ makes an angle $\beta$ with $v_A$, then $$\tan\beta=\frac{v_B\sin\theta}{v_A-v_B\cos\theta}$$

Visit Motion in a straight line formulas page and get all the formulas of this chapter, a pdf file is also available for download.