Introduction to the concept of trajectory
A trajectory is a path followed by an object with mass in curvilinear motion (curved path) as a function of time.
Mathematically, It is defined by the equation in x-y coordinates.
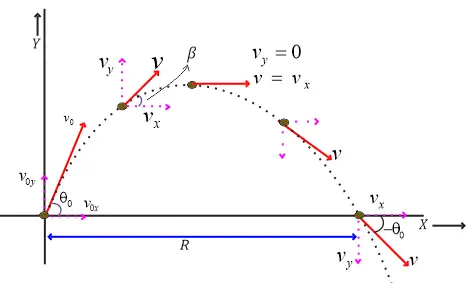
A famous example would be projectile motion like the ball thrown at an angle or a bullet fired from a gun. Here the path traveled by the ball or bullet followed a curvilinear motion under the influence of gravitational force. The path of the motion of the ball or bullet is the trajectory of the ball or bullet. Here we know that trajectory in these cases is a parabola
How to Find the trajectory of the motion
Example -1
A object moves such that its x and y coordinates varies as given below
$x=at$ -(1)
$y=b -ct$ -(2)
Here the trajectory of the object can be found by eliminating time from the equation
From equation (1)
$t= \frac {x}{a}$
Substituting these values in equation (2), we get
$y=b – c(\frac {x}{a})$
The above equation is called the trajectory of the object
Example-2
X-coordinate at any point
$x=(v_0cos{\theta _0})t$ -(1)
Y-coordinate at any point
$y=(v_0 \sin{\theta _0})t- \frac {1}{2}gt^2$ –(2)
Here the trajectory of the object can be found by eliminating time from the equation
From equation (1)
$t=\frac {x}{(v_0 \cos{\theta _0})}$
Substituting these values in equation (2), we get
$y=(\tan{\theta _0})x-[\frac {g}{2(v_0 \cos{\theta _0})^2}]x^2$
Example -3
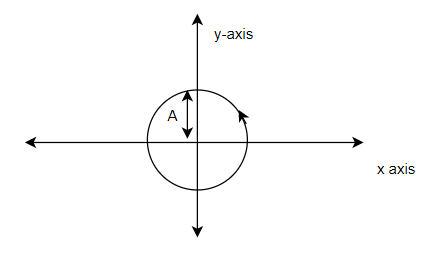
A object moves such that its position vector varies as
$R=(A \sin \omega t)i+(A \cos \omega t)j$
So $x=A \cos \omega t$ -(1)
$\cos \omega t=\frac {x}{A}$
$y=A \sin \omega t$ -(2)
$\sin \omega t=\frac {y}{A}$
Now we know that
$\sin^2 \omega t+ \cos^2 \omega t=1$
So, $(\frac {x}{A})^2+(\frac {y}{A})^2=1$
$x^2+y^2=A^2$
Which is a equation of a circle
