

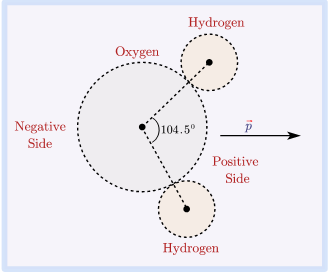
Electric dipole moment occurs when there is a separation of charge. It can occur in electrically neutral molecules with ionic bonds or molecules with covalent bonds. Dipole moments measures the electric polarity of system of charges.
Electric dipole moment measures the strength of an electric dipole. It is a vector quantity.
Electric dipole moment definition :- The dipole moment of an electric field is a vector whose magnitude is charge times the separation between two opposite charges.
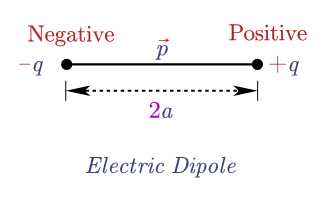
Answer: If charge \(q\) gets larger and the distance \(2a\) gets smaller and smaller such that the dipole moment, \(p=2\times 2a\) has finite value then such a dipole of negligibly small size is called an ideal or point dipole
