Given below are the Class 10 Maths Real Numbers Worksheets
a. HCF and LCM problems
b. Prime Factorisation Problems
c. Fundamental Theorem of Arithmetic method Problems
d. Long answer questions
e. Word Problems
Short Answer type
Question 1 Use Euclid algorithm to find the HCF of 4052 and 12576. Solution
Question 2
What is the smallest number that, when divided by 35, 56 and 91 leaves remainders of 7 in each case? Solution
LCM of 35, 56 and 91= 3640
Hence the number is =3640+7=3647
Question 3
show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer. Solution
Let a be any odd positive integer and b=4.
By division lemma there exist integer q and r such that
a = 4 q + r, where 0 ≤ r < 4
or a = 4q or, a = 4q +1 or, a = 4q + 2 or, a = 4q +3
Now 4q and 4q+2 are even numbers
so a= 4q +1 or, a = 4q +3
Hence , any odd integer is of the form 4q + 1 or, 4q +3.
Question 4
LCM of two numbers is 2295 and HCF is 9. If one of the numbers is 153, find the other number. Solution
HCF x LCM= Product of the Numbers
Hence the other number is = (2295 * 9)/153=135
Question 5
Express 111972 as a product of its prime factors. Solution
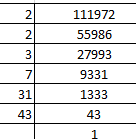
111972=2 * 2 * 3 * 7 * 31 * 43
Question 6
Find HCF and LCM of following using Fundamental Theorem of Arithmetic method.
448, 1008 and 168 Solution
Question 7
Find the HCF and LCM of following using Fundamental Theorem of Arithmetic method 377, 435 and 667. Solution
HCF=29
LCM=30065
Question 8
Using prime factorization method, find HCF and LCM of 80, 124 and 144. Also, show that HCF X LCM =Product of three numbers. Solution
HCF=4
LCM=22320
Question 9
Find the least positive integer which when diminished by 5 is exactly divisible by 36 and 54. Solution
For this we have to find L.C.M of 36 and 54.
L.C.M. of 36 and 54 = 2*2*3*3*3 = 108
Now,
The least number = (L.C.M. of 36 and 54) + 5
=108+5 = 113
Hence 113 is the least positive integer which on diminished by 5 is exactly divisible by 36 and 54.
Question 10
Find HCF and LCM of 12, 63 and 99 using prime factorisation method. Solution
HCF=3
LCM=2772
Question 11
If the HCF of 144 and 180 is expressed in the form 13m – 3, find the value of m. Solution
144=$2^4 \times 3^2$
Question 12
Three alarm clocks ring at intervals of 4, 12 and 20 minutes respectively. If they start ringing together, after how much time will they next ring together? Solution
Here we need to find the LCM for the numbers 4,12,20
By prime factorisation
4= 22
12=22*3
20= 22*5
LCM = 22*3*5=60 min
Question 13
In sports Day activities of a school, three cyclists start together and can cycle 48 km, 60 km and 72 km a day round the field. The field is circular, whose circumference is 360 km. After how many rounds they will meet again? Solution
Here we need to find the LCM for the numbers 48,60,72
By prime factorisation
48= 24*3
60=22*3*5
72= 23*32
LCM = 24*32*5=720 km
So 2 rounds
Long Answer type
Question 14
Two tankers contain 850 litres and 680 litres of petrol respectively. Find the maximum capacity of tanker which can measure the petrol of either tanker in exact number of times. Solution
The capacity of required container will be obtained by finding the HCF of the capacity of tankers
By prime factorisation
850 = 2×52*17
680 = 23*5*17
HCF = 2*5*17
= 170 Litres
Question 15
The traffic lights at three different road – crossing change after every 36 seconds, 60 seconds and 72 seconds. If they change simultaneously at 8 a. m. after, what time will they change again simultaneously? Solution
Given that traffic light at three different road crossing change after every 36 seconds,60 seconds and 72 seconds respectively.
36 = 2 * 2 * 3 * 3
60 = 2 * 2 * 3 * 5
72 = 2 * 2 * 2 * 3 * 3
Hence LCM of 36, 60 and 72 = (2 * 2 * 2 * 3 * 3 * 5)
= 360
That is after 360 seconds(5 Min) they will change simultaneously
Thus the traffic lights change simultaneously at 8:05 am
Question 16
Find HCF of numbers 134791, 6341 and 6339 by Euclid’s division algorithm. Solution
HCF=1
Question 17
Determine the prime factorization of 45470971 positive integers. Solution
2 Â Â 132 Â 172 Â 19
Question 18
A rectangular courtyard is 18m 72 cm long and 13m 20cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles. Solution
length of rectangular courtyard = 18 m 72 cm =18X100 +72= 1872 cm
Width of rectangular courtyard = 13 m 20 cm=13X100+20= 1320 cm
To find the square tile of maximum side we take the HCF of 1872 and 1320
By Euclid’s division lemma we have
1872 = 1320 * 1 + 552
1320 = 552 * 2 + 216
552 = 216 * 2 + 120
216 = 120 * 1 + 96
120 = 96 * 1 + 24
96 = 24 * 4 + 0
Hence the HCF is 24
Therefore maximum side of the square = 24 cm
Number of tiles required = (Area of rectangular courtyard)/(Area of square tile)
= (1872 * 1320)/(24 * 24)
= 4290
Question 19 Find the least number that is divisible by all the numbers between 1 and 10 (both inclusive). Solution
The least number divisible by all the numbers from 1 to 10 will be the LCM of these numbers.
By prime factorisation
1 = 1
2 = 2 * 1
3 = 3 * 1
4 = 22
5 = 5 * 1
6 = 2 * 3
7 = 7 * 1
8 = 23
9 = 32
10 = 2 * 5
LCM= 1 * 2 * 2 * 2 * 3 * 3 * 5 * 7 = 2520
Summary
This Class 10 Maths Real Numbers Worksheets with answers is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail.
link to this page by copying the following text Also Read
