

Given F=3 N
m=.1 kg
$F=ma$
or
$a = \frac {F}{m}= 30$ m/s2
Given F=7 N,m=400g= .4 kg
Acceleration is given by
$a= \frac {F}{m}$
a=17.5 m/s2
Now u=0,v=80 m/s
$v=u + at$
$t=\frac {v-u}{a}$
t=4.57 sec
As m=0, F=0
Hence (a) is correct
(d) as there is no friction force

Velocity can find using
$v=u+at$
For u=0
$v=at$
Momentum
$P=mv$

$F=ma$
Given a=4.00 m/s2
m=1000kg
Therefore , $F= ma= 1000 \times 4 =4000$ N
Given $\Delta v=4 m/s$ ,t=4 s ,m=1kg
Acceleration is given by
$a= \frac {\Delta v}{t}$
a=1 m/s2
Now force is given by
$F=ma$
F=1 N
$F=ma$
or
$a= \frac {F}{m}$
or
a= -500/200=-2.5 m/s2
Now
$v^2=u^2 +2as$
Now v=0,s=20 m,a=-2.5 m/s2
So, u=10 m/s
$F_1= ma_1$
and
$F_2=ma_2$
So,Ratio of force exerted is given by
$=\frac {F_1}{F_2}=\frac {ma_1}{ma_2}=\frac {a_1}{a_2}= 1:2$
The impulse experienced by an object is given by the change in momentum. Mathematically, impulse (I) is defined as: \[ I = \Delta p \] where \( \Delta p \) is the change in momentum. The momentum (p) of an object is given by the product of its mass (m) and velocity (v): \[ p = m \cdot v \] So, the change in momentum is: \[ \Delta p = m \cdot \Delta v \] In this case, the cricket ball is stopped, so the final velocity (\( v_f \)) is 0 m/s. Therefore, the change in velocity (\( \Delta v \)) is: \[ \Delta v = v_f - v_i \] where \( v_i \) is the initial velocity. Now, calculate the impulse: \[ I = m \cdot \Delta v \] \[ I = m \cdot (v_f - v_i) \] \[ I = (0.20 \, \text{kg}) \cdot (0 - 1.2 \, \text{m/s}) \] \[ I = -0.24 \, \text{Ns} \] The negative sign indicates that the direction of the impulse is opposite to the initial velocity. Now, to find the average force (\( F \)) applied by the player, you can use the formula: \[ F = \frac{I}{\Delta t} \] where \( \Delta t \) is the time over which the force is applied. In this case, \( \Delta t = 0.10 \, \text{s} \): \[ F = \frac{-0.24 \, \text{Ns}}{0.10 \, \text{s}} \] \[ F = -2.4 \, \text{N} \] The negative sign indicates that the force is applied in the opposite direction to the initial motion of the ball.
$ \Delta P= m \times (v - u) = 0.2 \times (-2 - 10) = -2.4$ kg ms-1
(The negative sign indicates a change in direction of hockey ball after it is struck by hockey stick. )
Given $m_1 = 100 gm = 0.1 kg$, $m_2 = 200 gm = 0.2 kg$
$u_1 = 2$ ms-1, $u_2 = 1$ ms-1, $v_1 = 1.67$ ms-1, $v_2 = ?$
By the law of conservation of momentum,
$m_1 u_1+m_2 u_2=m_1 v_2 + m_2 v_2$
$0.1 \times 2+ 0.2 \times 1=0.1 \times 1.67 + 0.2 v_2$
$v_2 = 1.165$ ms-1
It will move in the same direction after collision
Impulse=Change in Momentum= 10 Kgm/s
Let v be the initial recoil velocity of the rifle
From law of conservation of Momentum
$0=.01 \times 20 + 4 \times v$
Or $v=-.05 m/s$
we have $F = ma$.
Here we have $m_1 = 2$ kg and $a_1 = 5 m/s^2$
and $m_2 = 6$ kg and $a_2 = 2 m/s^2$ .
So,
$F_1 = m_1a_1 = 2 \times 5 = 10 N$
$F_2 = m_2a_2 = 6 \times 2 = 8 N$.
Here $F_1 < F_2$
Thus, accelerating a 6 kg mass at 2 m/s2 would require a greater force
From Force formula
$F=ma$
$5=8m_1$ or $m_1= \frac {5}{8}$
and $5= 24m_2$ or $m_2 = \frac {5}{24}$
Now when the two masses are tied and same force is applied, acceleration will be
$a = \frac {F}{m_1+ m_2} = \frac {5}{\frac {5}{8} + \frac {5}{24}} = 6 m/s^2$
Acceleration of the Hammer is given by
$a = \frac {v-u}{t} = \frac {0- 50}{.01}= -5000 m/s^2$
Force is given by
$F=ma = .5 \times 5000 = 2500N$
Total mass, m = mass of engine + mass of wagons
Or, $m = 8000 + 5 \times 2000 = 18000$ kg.
(a) The net accelerating force, F = Engine force - Frictional force
Or, F = 40000 - 5000 = 35000 N
(b) The acceleration of the train
$a= \frac {F}{m}=\frac {35000}{18000}=1.94$ m/s2
(c) The force of wagon 1 on wagon 2
Assuming Frictional Force on all the wagons and engine
Frictional resistance of 4 wagons = $ \frac {5000 \times (2000 \times 4)}{18000} =2222 .22 N$
Accelerating force on 4 wagons =$2000 \times 4 \times 1.944 =15552 N$
Hence total force exertred by wagon on wagon 2= Accelerating force +Frictional resistance
$=2222 .22 +15552=17774.22 N$
Assumining frictional force on engine only
Accelerating force on 4 wagons =$2000 \times 4 \times 1.944 =15552 N$
i. u=103 m/s ,v=0 ,s=5 cm= .05 m ,a=?
$v^2=u^2 + 2as$
a=- 107 m/s
Resistive force on bullet = $.001 \times 10^7= 10^5 N$
ii. $v=u+at$
t=104s
$M_a=100$ kg, $M_b=75$ kg , $v_a =40 km/hr$, $v_b=6 km/hr$
a. Now $M_a > M_b$, So Object A has more inertia
b. $p_a= M_a v_a= 4000 kg km/hr $, $p_b= M_b v_b= 450 kg km/hr $
Clearly $p_a > p_b$
c. Since velocity of object B is less then velocity of object A, Object B will stops first if equal negative acceleration is applied on both
d. Object A
e. Object A
Given u=0 ,v= 54 km/hr= 15 m/s , t=2 sec
a. Acceleration is given by
$a=\frac {\Delta v}{t}$
So, a=7.5 m/s2
b. Distance is given by
$s=ut+ \frac {1}{2}at^2$
s= 15 m
c. Force is given by
$F=ma=1000 \times 7.5=7500$ N
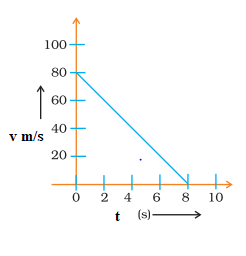
From the graph ,we can see that
$\Delta v=-80 m/s$, t=8 sec
Now
$a= \frac {\Delta v}{t} = -10 m/s^2$
Frictional force will be given as
$F= ma= .1 \times -10 = -1 N$
By using law of conservation of momentum
$m_1u_1 = (m_1 + m_2)v$
$.01 \times 400 = .91 v$
v=4.39 m/s
Here m= 60 kg ,u1= 18 km/hr = 5 m/s , M=100 kg ,u2=0
Let v be the velocity with car start travelling
Now
$mu_1 + Mu_2 = (M+m)v$
$ 60 \times 5 = 160 v$
v= 1.875 m/s
This numericals on force and laws of motion for class 9 is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail.