physicscatalyst.com logo




Latest Articles

Class 9 Science Chapter 10 – Gravitation online Test
Online Test for Class 11 Physics Mechanical Properties of Fluids
quadratic equation Class 10 test paper
Class 9 Maths Chapter -3 Coordinate Geometry MCQs
Arithmetic Progression Quiz

Cardinality of the set





Cardinality of the set

  • The cardinality of the set defines the number of element in the Set
  • If \(A\) is the set, Cardinality of the set is defined as \(n(A)\)
  • For \(A = \{ 1,2,3\} \) then \(n(A) = 3\)

Set Relations

Joined Set Disjoined Set
Set having common elements Set having no common elements
\(n\left( {X \cap Y} \right) \ne 0\) \(n\left( {X \cap Y} \right) = 0\)

Important Operation on Cardinality

  1. If \(n\left( {X \cap Y} \right) \ne 0\)
    \(n\left( {X \cup Y} \right) = n\left( X \right) + n\left( Y \right) - n\left( {X \cap Y} \right)\)
  2. If \(n\left( {X \cap Y} \right) = 0\)
    \(n\left( {X \cup Y} \right) = n\left( X \right) + n\left( Y \right)\)
  3. if X, Y and Z are finite set
    $n ( X \cup Y \cup Z ) = n ( X ) + n ( Y ) + n ( Z ) - n ( X \cap Y ) - n ( Y \cap Z) - n ( X \cap Z ) + n ( X \cap Y \cap Z )$

Cardinality of empty set

  • Cardinality of empty set is zero
  • if $A = \phi $,then n(A)=0

Cardinality of Power set

  • Cardinality of power set of A is given by $2^m$ where m is the Cardinality of set A
  • if $n(A) = \phi $,then n[P(A)]=1



Question 1
If A and B are two sets such that A ∪ B has 50 elements, A has 28 elements and B has 42 elements, how many elements does A ∩ B have
Solution
\(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\)
50=28+42-x
x=20

Question 2
Sets A and B have 12 and 8 elements respectively. What can be the minimum number of elements in $A \cup B$
Solution
We know that
\(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\)
$A \cup B = 12 + 8 - n(A \cap B)$
Now maximum number of elments possible in $A \cap B $ = 8 ( B is subset of A)
So, Minimum number of elements in $A \cup B$ = 12 + 8 -8 =12
Question 3
A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 58 men and only three men got medals in all the three sports, how many received medals in exactly two of the three sports ?
Solution
Let F, B and C denote the set of men who received medals in football, basketball and cricket, respectively.
Then ,According to the questions, we have
n ( F ) = 38, n ( B ) = 15, n ( C ) = 20 ,$n (F \cup B \cup C ) = 58$ and $ (F \cap B \cap C ) = 3$
Now,
$n (F \cup B \cup C ) = n ( F ) + n ( B )+ n ( C ) - n (F \cap B ) - n (F \cap C ) - n (B \cap C ) \\ + n ( F \cap B \cap C )$
$58=38+15+20 -(n ( F \cap B ) + n ( F \cap C ) + n ( B \cap C ) ) +3$
or $n ( F \cap B ) + n ( F \cap C ) + n ( B \cap C ) = 18$ -(1)

Now the question is asking for exactly two of the three sports ie.
$n (( F \cap B ) -C) + n (( F \cap C ) -B) + n (( B \cap C )-F)$
=$n ( F \cap B ) + n ( F \cap C ) + n ( B \cap C ) -3 (F \cap B \cap C )$
=18 -9 =9

We can understand this with Venn diagram also

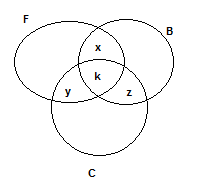
Here, x denotes the number of men who got medals in football and basketball only, y denotes the number of men who got medals in football and cricket only, z denotes the number of men who got medals in basket ball and cricket only and k denotes the number of men who got medal in all the three.
Now ,
$F \cap B = x+k$
$F \cap C = y+k$
$B \cap C = z+k$

We need to find a+b+c
Now as per equation (1)
x +k + y + k + z + k = 18
Therefore a + b + c = 9

Quiz Time

Question 1 if set $A= \phi$,then how many elements will be present in power set of A
A) 1
B) 0
C) 2
D) 3
Question 2 If P and Q are two sets such that P ∪ Q has 30 elements, P has 12 elements and Q has 18 elements, how many elements does P ∩ Q have ?
A) 12
B) 18
C) 0
D) None of the above
Question 3 what is the cardinality of the set $A= {x| x \; is \; a \; positive \; integer \; less \; than \; 10 \; and \; 2^x - 1\; is\; an\; odd \;number}$
A) 10
B) 8
C) 9
D) 0
Question 4 In a class of 120 students numbered 1 to 120, all even numbered students opt for Hockey, those whose numbers are divisible by 5 opt for football and those whose numbers are divisible by 7 opt for Badminton. How many opt for none of the three sports?
A) 21
B) 50
C) 19
D) 41
Question 5 A = { 1,2,3,4,5} and B ={2,3,4,5} then which of below is false
A) n(A - B) =1
B) n(B -A) =1
C)n(A ∪ B) =5
D)n(A ∩ B)=4
Question 6In a survey of 400 students in a school, 100 were listed as Cricket, 150 as taking Football and 75 were listed as taking both Football as well as cricket. Find how many students were taking neither cricket nor football
A) 200
B) 225
C) 100
D) 0


Also Read




Latest Updates
Synthetic Fibres and Plastics Class 8 Practice questions
Class 8 science chapter 5 extra questions and Answers
Mass Calculator
3 Fraction calculator
Garbage in Garbage out Extra Questions7



Physicscatalyst

Our aim is to help students learn subjects like physics, maths and science for students in school , college and those preparing for competitive exams.

Other Links

Legal

Email us at

[email protected]

© 2007-2019 . All right reserved. All material given in this website is a property of physicscatalyst.com and is for your personal and non-commercial use only