Light Reflection and Refraction Class 10 Numericals
Welcome to this page on Numericals on Light for Class 10 Science chapter 10. These questions will help you improve your ranks with the great collection of Numericals on Light Class 10 of 3 marks questions. These light reflection and refraction class 10 questions and answers are from various topics and formulas like
Mirror Formula
Lense Formula
Refractive index etc.
We also have light class 10 notes written in simple language to assist students with their studies. Please do check them out for more information.
Light Class 10 Numericals
Question 1. A coin placed at the bottom of a tank appears to be raised when water is poured into it. Explain. click for answer
Answer 1. This occurs due to the, phenomenon of refraction of light. Here, the ray of light from the coin travels from a denser medium to a rarer medium . In this process it bends away from the normal . The point from which the refracted rays appear to come gives the apparent position of the coin. As the rays appear to come from a point above the coin, so, the coin seems to be raised.
Question 2. A 5 cm tall object is placed perpendicular to the principal axis of a convex lens of focal- length 20 cm. The distance of the object from the lens is 30 cm. Find the:
(i) position
(ii) nature
(iii) size of the image formed. click for answer
Answer 2.
Given object size = 5 cm
object distance from lens $u = -30$ cm
focal length $f = 20$ cm,
We have to find $v = ?$
Using the lens formula $\frac{1}{f} = \frac{1}{v}-\frac{1}{u}$
We have,
$ \frac{1}{v} = \frac{1}{u} + \frac{1}{f} = \frac{1}{-30} + \frac{1}{20} = \frac{ -2+3 }{ 60 } = \frac{1}{60}$
or,
$\frac{1}{v} = \frac{1}{60}$
Thus
$v = 60cm$ . This is part (i) of the question
magnification
$\frac{v}{u} = \frac{60}{-30} = -2 $
$Magnification \quad = \quad \frac{Image \quad size}{Object \quad size}$
$\frac{h_i }{h_o}=-2 $
$\frac{h_i}{5}=-2$
$h_{i}= -2 \times 5 = -10 \quad cm$
The image is real inverted and magnified.
Question 3. (a) Write two rules of the new Cartesian sign conventions for spherical mirrors.
(b) Trace the path of the reflected ray by drawing a figure if it passes from centre of curvature of a concave mirror. click for answer
Answer 3.
(1) New Cartesian sign conventions for measuring the various distances in the ray diagrams (reflection by spherical mirrors)
1. All the distances in a ray diagram are measured from the pole of the spherical mirror.
2. The distances measured in the direction of incident light are taken as positive.
3. The distances measured in the direction opposite to the direction of incident light are taken as negative.
4. The heights measured upwards and perpendiculars to the principal axis of the mirror are taken as positive.
5. The heights measured downwards and perpendiculars to the principal axis of the mirror are taken as negative.
Answer 3.
(2) Visit page https://physicscatalyst.com/Class10/light-reflection-and-refraction.php#spherical-mirrors
Question 4. Design an activity using concave mirror to prove that it s converging in nature. Also state a method to find its rough focal length. click for answer
Answer 4
The following activity can be used to determine the principal focus and approximate focal length of a concave mirror.
(1) Place the mirror vertically on a table.
(2) Place an object (a pencil) in front of the mirror and move it towards and away from the mirror.
(3) Find the approximate spot where the reflection of the object changes from upright to upside down. This point is the focus of the mirror. Measure the distance between this point and the mirror. This length is the focal length of the mirror.
Question 5. 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of image and magnification. Describe what happens to the image as the needle is moved farther from the mirror. click for answer
Answer 5
Given that $h_1 = 4.5 \quad cm,\quad u = - 12 cm, \quad f = 15 cm$
We have to find $ v = ?$
using the equation of the mirror formula $\frac{1}{f} = \frac{1}{v}+\frac{1}{u}$
we have,
$\frac{1}{15} = \frac{1}{v}+\frac{1}{-12}$
$\frac{1}{15}+\frac{1}{12}=\frac{1}{v}$
By solving we get v= +6.6 cm.
Now, magnification
$m= \frac{h_2}{h_1}=-\frac{v}{u}$
Thus,
$h_2 = - \frac{v}{u} \times h_1 = \frac{-6.6}{-12} \times 4.5 = +2.5 \quad cm$
Hence, magnification of image,
$m=\frac{h_2}{h_1} = \frac{2.5}{4.5} = .56$
The height of the image is 2.5 cm. The positive sign indicates that the image is erect, virtual, and diminished.
Question 6. Rohit placed a pencil perpendicular to principal axis in front of a converging mirror of focal length 30 cm. The image formed is twice the size of the pencil. Calculate the distance of the object from the mirror. click for answer
$Magnification = \frac {h_i}{h_o}=-\frac {v}{u}$
For real image
$m=-\frac {v}{u} =-2$
v=2u
Now Using the mirror equation,
$\frac {1}{v} + \frac {1}{u}=\frac {1}{f}$
$\frac {1}{2u} + \frac {1}{u} =\frac {1}{-30}$
u=-45 cms. which is between the focal length and the Curvature.
For virtual image
$m=-\frac {v}{u} =2$
v=-2u
Now Using the mirror equation,
$\frac {1}{v} + \frac {1}{u}=\frac {1}{f}$
$\frac {1}{-2u} + \frac {1}{u} =\frac {1}{-30}$
u=-15 cm which is between the focal length and the pole
Question 7. Define magnification produced by a spherical mirror in terms of height of a object and image. How is it related to object and image distance? Explain why magnification is positive for virtual image and negative for real image? click for answer
Answer 7
Linear magnification is the ratio of the height of the image to the height of the object. It is represented by the letter $m$
$m=\frac{height \quad of \quad image}{ height \quad of \quad object} = \frac{h_i}{h_o}$
where, $h_i$ is the height of image and $h_o$ is the height of object.
If the image formed is virtual and erect, then the magnification is positive. If the image formed is real and inverted, then the magnification is negative.
Question 8. An object is placed at a distance of 25 cm away from a converging mirror of focal length 20 cm. Discus the effect on the nature and position of the image if the position of the object changes from 25 cm to 15 cm. Justify your answer without using mirror formula. click for answer
If the object is placed at 25 cm in front of the concave mirror having focal length 20 cm, this means that the object is placed in between focus and the centre of curvature of the mirror. If the object is placed in front of the center of curvature then the image will be formed beyond the centre of curvature.So the image formed is a real image. The nature of the image will be will be inverted and enlarged
If the object is placed at 15 cm in front of the concave mirror having focal length 20 cm, this means that the object is placed in between focus and the pole of the mirror. An object placed between the pole and focus of a concave mirror forms a virtual image.The nature of the image will be will be erect and enlarged
Question 9. Write one similarity and one dissimilarity between image formed by plane mirror and convex mirror. click for answer
Answer 9
Similarity :- Both produce Virtual Image .
dissimilarity :- Convex Mirror produces diminished image while plane mirror produce the Image of the same size as that of the object .
Question 10. (a) State Snell’s law of refraction.
(b) When a ray of light travelling in air enters obliquely into a glass slab, it is observed that the light ray emerges parallel to the incident ray but it is shifted sideways slightly. Draw a ray diagram to illustrate it. click for answer
Answer 10
snell' law of refraction is:- "the ratio of sine of angle of incident to sine of angle of refraction is always constant for given medium"
where,
$\frac{{\sin i}}{{\sin r}} = constant = {n_{12}}$
where, $n_{12}$ = refractive index of medium 2 with respect to the medium 1.
The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence , all lie in the same plane.
Question 11. A 5cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 10 cm. The distance of the object from the lens is 15 cm. Find the nature, position and size of the image. Also find its magnification. click for answer
$h_o=5 cm$, f=10 cm , u=-15 cm ,v=?
Using lens formula
$\frac {1}{f}=\frac {1}{v} - \frac {1}{u}$
$\frac {1}{10} = \frac {1}{v}- \frac {1}{-15}$
or v=30 cm
Now $m =\frac { v}{u} = -2$
Now
$\frac {h_i}{h_o} = -2$
or $h_i= -10 cm$
So,image is real, inverted and enlarged
Question 12. One half of a convex lens is covered with a black paper.
(a)Show the formation of image of an object placed at 2F1, of such covered lens with the help of ray diagram. Mention the position and nature of image.
(b)Draw the ray diagram for same object at same position in front of the same lens, but now uncovered. Will there be any difference in the image obtained in the two cases? Give reason for your answer. click for answer
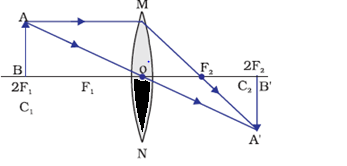
Complete image will be formed when the one half of a convex lens is covered with a black paper. Basically the other half refract to form the final image
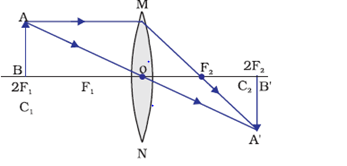
The image formation is shown above.
Full images are formed in both the cases. It is just the intensity of the image which is different.The intensity of image in Case 1 will be half of Case 2
Question 13. (a) The refractive index of Ruby is 1.71. What is meant by this statement?
(b) The refractive index of some medium are given below:
Crown glass- 1.52
Water- 1.33
Sapphire- 1.77
In which of the medium is the speed of light
(i)maximum
(ii)minimum
(iii) Calculate speed of light in sapphire. click for answer
a. Refractive index of an optical medium is ratio speed of the light in air to the speed of the light in the optical medium.So the refractive index of Ruby is 1.71 means ratio of speed of light in air to the speed of light in ruby is equal to 1.71
b. $Refractive \; Index = \frac {speed \; of \; light \; in \; air}{speed \; of \; light \;in \;optical\; medium}$
$speed \; of \; light \;in \;optical\; medium = \frac {speed \; of \; light \; in \; air}{Refractive \; Index}$
So higher the refractive index, lower the speed
So, Speed will be maximum in water and lowest in Sapphire
Now
$speed \; of \; light \;in Sapphire = \frac {speed \; of \; light \; in \; air}{Refractive \; Index\; of\; Sapphir}$
$= \frac {3 \times 10^8}{1.77} =1.69 \times 10^8 m/s$
Question 14. A 10 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 30 cm. The distance of the object from the lens is 20 cm. Find the:
(a)Position
(b)Nature
(c)Size of the image formed. click for answer
Given that f=30cm , u= -20cm , v=?
Using Lens formula
$\frac {1}{f} = \frac {1}{v} - \frac {1}{u}$
$ \frac {1}{30}=\frac {1}{v} - \frac {1}{-20}$
v = -60 cm
Hence the image is at a distance of 60 cm from the lens.The negative sign indicates it is on same side on lens as the object and it is a real image.
Now the size can be obtained using the magnification formula
$m=\frac {h_i}{h_o}=\frac {v}{u}$
$\frac {h_i}{10}= \frac {-60}{-20}$
$h_i=30cm$
Hence Position of image is 60 cm on same side of lens and image is 30 cm and it is erect image
Question 15. Draw a ray diagram to show refraction of light through a glass slab and label on it the following:
(i)Incident ray
(ii)Refracted ray
(iii)Emergent ray
(iv)Lateral shift (displacement) Question 16. If the image formed by mirror for all positions of the object placed in front of it is always virtual and diminished, state the type of the mirror. Draw a ray diagram in support of your answer. Where are such mirrors commonly used and why? click for answer
The answer is convex mirror as its forms an erect diminished virtual image for all the positions of the object placed in front of it.
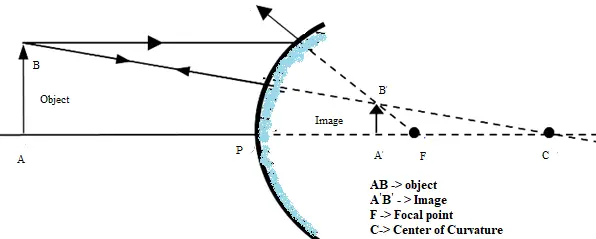
A convex mirror is used as rear view mirrors in auto-mobiles, as reflectors in street light bulbs and in parking lots.
Question 17. A 6 cm object is placed perpendicular to the principal axis of a convex lens of focal length 15 cm. The distance of the object from the lens is 10 cm. Find the position, size and nature of the image formed, using the lens formula. click for answer
Given that f=15cm , u= -10cm , v=?
Using Lens formula ,
$\frac {1}{f} = \frac {1}{v} - \frac {1}{u}$
$ \frac {1}{15}=\frac {1}{v} - \frac {1}{-10}$
v = -30 cm
Hence the image is at a distance of 30 cm from the lens.The negative sign indicates it is on same side on lens as the object and it is a real image.
Now the size can be obtained using the magnification formula
$m=\frac {h_i}{h_o}=\frac {v}{u}$
$\frac {h_i}{6}= \frac {-30}{-10}$
$h_i=18cm$
Hence Position of image is 30 cm on same side of lens and image is 18 cm and it is erect image
Question 17.
The ability of a medium to refract light is expressed in terms of its optical density. Optical density has a definite connotation. It is not the same as mass density. On comparing two media, the one with the large refractive
index is optically denser medium than the other. The other medium with a lower refractive index is optically rarer. Also the speed of light through a given medium is inversely proportional to its optical density.
(i) Determine the speed of light in diamond if the refractive index of diamond with respect to vacuum is 2.42. Speed of light in vacuum is $3 \times 10^8$m/s.
(ii) Refractive indices of glass, water and carbon disulphide are 1.5, 1.33 and 1.62 respectively. If a ray of light is incident in these media at the same angle (say $\theta$), then write the increasing order of the angle
of refraction in these media.
(iii) (A) The speed of light in glass is $2 \times 10^8$ m/s and in water is $2.25 \times 10^8$ m/s.
(a) Which one of the two is optically denser and why ?
(b) A ray of light is incident normally at the water-glass interface when it enters a thick glass container filled with water. What will happen to the path of the ray after entering the glass ? Give reason.
(iv) (B) The absolute refractive indices of water and glass are 4/3 and 3/2 respectively. If the speed of light in glass is $2 \times 10^8$ m/s, find the speed of light in (i) vacuum and (ii) water. click for answer
(i) $n_d = \frac {v_{vaccum}}{v_{diamond}}$
or $v_{diamond} = \frac {v_{vaccum}}{n_d} = 1.25 \times 10^8$ m/s
(ii) $r_w$ < $r_{g}$ < $r_{c}$
(iii)(a)since speed is glass is less than water, Glass is optically densor
(b)it will go normal. as angle of incidene is 0 ,so the angle of refraction will be zero
(iii)for Glass
$n_g = \frac {v_{vaccum}}{v_{glass}}$
$\frac {3}{2}= \frac {c}{2 \times 10^8}$
or $c=3 \times 10^8$ m/s.
For water
$n_w = \frac {v_{vaccum}}{v_{water}}$
$v_{water}= \frac {c}{4/3}$
or $c=2.25 \times 10^8$ m/s
Question 18.
It is desired to obtain an erect image of an object, using concave mirror of focal length of 12 cm.
(i)What should be the range of distance of an object placed in front of the mirror?
(ii)Will the image be smaller or larger than the object? Draw ray diagram to show the formation of image in this case,.
(iii)Where will the image of this object be, if it is placed 6 cm in front of the mirror? Draw ray diagram for this situation to justify your answer.
Show the position of pole, principal focus and the centre of curvature in the ray diagram. Answers
(i) In concave mirror erect is formed only when the object is placed between pole and focus. So object distance should be less than 12 cm
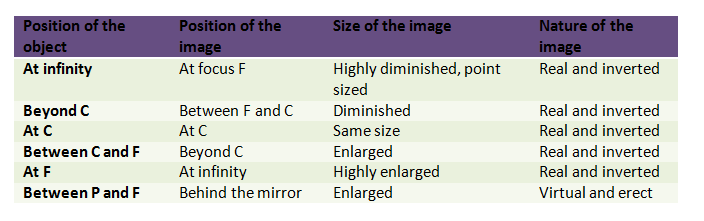
(ii) The image would be larger than the object
(iii) Here u=-6 cm , f=-12 cm
Using Mirror Formula
$\frac {1}{f} =\frac {1}{v} + \frac {1}{u}$
$\frac {1}{-12} =\frac {1}{v} + \frac {1}{-6}$
v= 12 cm
Question 19.
A student has three concave mirrors A, B and C of focal lengths 20 cm, 15 cm and 10 cm respectively. For each concave mirror he performs the experiment of image formation for three values of object distance of 30 cm, 10 cm and 20 cm.
Giving reason answer the following:
(a)For the three object distances, identify the mirror which will form an image equal in size to that of object. Find at least one value of object distance.
(b)Out of the three mirrors, identify the mirror which would be preferred to be used for shaving purpose.
(c)For the mirror B, draw ray diagram for image formation for any two given values of object distance. Answers
Given
$f_A=20 cm$,$f_B=15 cm$,$f_C=10 cm$,$u_1=30 cm$,$u_2=10 cm$,$u_3=20 cm$
a. For same size image, object should be placed at Center of Curvature
So for Mirror A, Image will not of same size for these positions
For Mirror B,Image will be of same size for position $u_1=30 cm$
For mirror C,Image will be of same size for position $u_3=20 cm$
b.We need enlarged and erect image for shaving. For erect and enlarged image, Object should be placed between Pole and Focus. Face would be generally kept at more than 10 cm distance, so mirrors A and B are suitable for shaving
Question 20.
An object is placed at infinity from a concave mirror of focal length 10 cm. Find the position and nature of image formed. Draw a ray diagram to show the formation of image. (Not to scale) Answers
Image formed at 10 cm in front of concave mirror,inverted,smaller than object.
Question 21.
(a) Define focal length of a spherical lens.
(b) A divergent lens has a focal length of 30 cm. At what distance should an object of height 5 cm from the optical centre of the lens be placed so that its image is formed 15 cm away from the lens? Find the size of the image also.
(c) Draw a ray diagram to show the formation of image in the above situation. Answers
(a) check this Refraction by Spherical Lenses
(b) f= -30 cm; $h_o = 5cm$ ,v=-15 cm
Using lens Formula,
$\frac {1}{f} = \frac {1}{v} -\frac {1}{u}$
$\frac {1}{-30} = \frac {1}{-15} -\frac {1}{u}$
u=-30 cm
Now
$ \frac {v}{u}=\frac {h_i}{h_o}$
or
$h_i = \frac {v \times h_o}{u} = 2.5 cm$
Question 22.
(a) A converging lens forms a real and inverted image of an object at a distance of 100 cm from it. Where should an object be placed in front of the lens, so that the size of the image is twice the size of the object? Also, calculate the power of a lens.
(b) State laws of refraction. Answers
a. Since this is converging lens, it is a convex lens
v=+100 cm
Now Magnification for lens is given by
$m= \frac {v}{u} =\frac {h_i}{h_o}$
Since the image is inverted
$\frac {v}{u} =-2$
or u =-50 cm
The object is placed at a distance 50 cm from the lens
Now using Lens formula
$\frac {1}{f} = \frac {1}{v} -\frac {1}{u}$
$\frac {1}{f} = \frac {1}{100} -\frac {1}{-50}$
or f=33.33 cm
Now
Power of the lens
$power = \frac {1}{f(m} = 3D$
Question 23.
List the new Cartesian sign convention for reflection of light by spherical mirrors. Draw a diagram and apply these conventions for calculating the focal length and nature of a spherical mirror which forms a 1/3 times magnified virtual image of an object placed 18 cm in front of it. Answers
a. check this Sign convention for reflection by spherical mirrors
b. Here u=-18 cm, m=1/3
Now $m= -\frac {v}{u}$
or v = 6 cm
Now using Mirror Formula
$\frac {1}{f} = \frac {1}{v} +\frac {1}{u}$
$\frac {1}{f} = \frac {1}{6} +\frac {1}{-18}$
f=9 cm.
Hence a convex mirror
Question 24.
a.One – half of a convex lens of focal length 110 cm is covered with a black paper. Can such a lens produce an image of a complete object placed at a distance of 30 cm from the lens? Draw a ray diagram to justify your answer.
b. A 4 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 20 cm. The distance of the object from the lens is 15 cm. Find the nature, position and size of the image. Answers
a. Yes
b. u=-15 ,f=20 cm ,v=?
Now using Lens formula
$\frac {1}{f} = \frac {1}{v} -\frac {1}{u}$
$\frac {1}{20} = \frac {1}{v} -\frac {1}{-15}$
v=-60 cm
Now $m= \frac {v}{u}=\frac {h_i}{h_o}$
or $h_i=16 cm$
So image is enlarged and erect
Summary
This Numericals on Light Class 10 Sciencewith answers is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail.
link to this page by copying the following text Also Read
